Діагональ куба: що це таке і як її знайти?
Діагональ куба — це один з елементів, що потрібно знати при вирішенні завдань по стереометрії під час виконання підсумкової роботи з математики за курс основної школи.
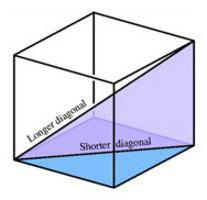 Всі шість граней куба являють собою квадрати. Довжина кожного з 12 ребер однакова. У кожній з граней можна провести діагональ, довжину якої легко знайти за формулою Піфагора. Крім того, сам куб має діагоналі. Їх усього чотири. Проводиться діагональ куба так, щоб починатися з вершини нижньої основи. Кінець цього відрізка виявляється у вершині верхнього підстави, але так, щоб не збігтися з діагоналлю квадрата.
Всі шість граней куба являють собою квадрати. Довжина кожного з 12 ребер однакова. У кожній з граней можна провести діагональ, довжину якої легко знайти за формулою Піфагора. Крім того, сам куб має діагоналі. Їх усього чотири. Проводиться діагональ куба так, щоб починатися з вершини нижньої основи. Кінець цього відрізка виявляється у вершині верхнього підстави, але так, щоб не збігтися з діагоналлю квадрата.
V= a3 (№1) використовується для знаходження об'єму; S= a2 (№2) формула для площі грані; S= 6a2 (№3) необхідна для розрахунку площі всієї поверхні куба; якщо потрібно дізнатися діагональ куба, формула буде такою d= а ? 3 (№4); для пошуку радіусів знадобляться: R= (а/2)* ?3 і r= а/2 (№5) і (№6) .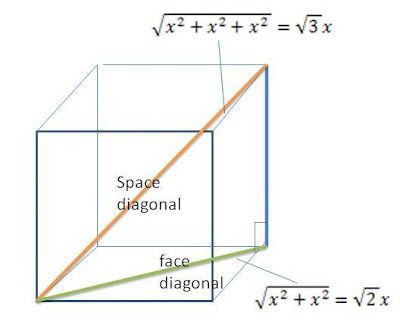
Перша група завдань. В ній відома довжина діагоналі куба. Потрібно обчислити його об'єм або дізнатися площа поверхні. Приміром, відома величина може дорівнювати одиниці. Тоді, щоб дізнатися обсяг і площа, потрібно скористатися формулами № 1 і 3. Але в них йде мова про ребрі, а дана діагональ. Потрібно записати ще одну формулу. Якщо подивитися на креслення куба і проведену в ньому діагональ, то можна побачити, що утворюється прямокутний трикутник. Один його катет збігається з ребром, другий - з діагоналлю межі, а гіпотенузою виявляється діагональ куба. Тоді можна записати теорему Піфагора: квадрат гіпотенузи (d 2 ) дорівнює квадрату першого катета (а 2 ), складеного з квадратом другого (а?2) 2 . Після виконання перетворень виходить, що ребро куба а так пов'язано з діагоналлю, що дорівнює d, поділеним на корінь квадратний з 3. Тепер можна початку дізнатися ребро, а потім підрахувати об'єм і площа. В конкретній задачі а=1/?3=(?3)/3. Тоді обсяг виходить рівним (?3)/9. Площа ж — два.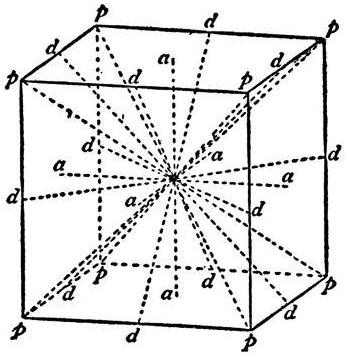 Друга група завдань. Протилежна попередній, коли відомі площа або об'єм, а потрібно обчислити значення діагоналі куба. Прикладом може служити задача, в якій відома площа поверхні, і вона дорівнює 8. Необхідно буде скористатися формулою №3 і тією залежністю, яка виведена в попередній задачі. Спочатку потрібно дізнатися довжину ребра. Вона дорівнює квадратному кореню з приватного S на 6. Після підстановки відомої величини а=?(8/6)=?(4/3). Тепер залишилося обчислити діагональ куба, звівши це число до квадрату і помноживши його на 3. Вийде 2. Третя група завдань містить дані про діагональ грані куба. В них необхідно дізнаватися об'єм або площа тіла. Можливий також варіант, у якому потрібно обчислити діагональ самого куба. У таких завданнях міркування йдуть тим же шляхом, який розглянуто в попередніх випадках.
Друга група завдань. Протилежна попередній, коли відомі площа або об'єм, а потрібно обчислити значення діагоналі куба. Прикладом може служити задача, в якій відома площа поверхні, і вона дорівнює 8. Необхідно буде скористатися формулою №3 і тією залежністю, яка виведена в попередній задачі. Спочатку потрібно дізнатися довжину ребра. Вона дорівнює квадратному кореню з приватного S на 6. Після підстановки відомої величини а=?(8/6)=?(4/3). Тепер залишилося обчислити діагональ куба, звівши це число до квадрату і помноживши його на 3. Вийде 2. Третя група завдань містить дані про діагональ грані куба. В них необхідно дізнаватися об'єм або площа тіла. Можливий також варіант, у якому потрібно обчислити діагональ самого куба. У таких завданнях міркування йдуть тим же шляхом, який розглянуто в попередніх випадках.
Трохи теорії про кубі
Цей багатогранник відноситься відразу до прямих параллелепипедам і призмах. Він - приватний випадок того й іншого. На підставі куба лежить квадрат, і бічні ребра його дорівнюють стороні даного квадрата. Таким чином, всі три виміри мають однакові значення.
Важливі формули
У них потрібно ввести однакову позначення. Найчастіше буква «а» — це сторона куба. «V» припадає на обсяг. «S» і «d» відповідно площа і діагональ. «R» і r» радіуси описаного і вписаного сфер.V= a3 (№1) використовується для знаходження об'єму; S= a2 (№2) формула для площі грані; S= 6a2 (№3) необхідна для розрахунку площі всієї поверхні куба; якщо потрібно дізнатися діагональ куба, формула буде такою d= а ? 3 (№4); для пошуку радіусів знадобляться: R= (а/2)* ?3 і r= а/2 (№5) і (№6) .

Кілька слів про симетрії куба
У цього геометричного тіла є два види симетрії: відносно точки і осі. Для знаходження першої потрібно провести діагональ куба, потім другу, щоб знайти точку їх перетину. Вона буде центром симетрії. Всі прямі, які проходять через цю точку і є перпендикулярними до граней, виявляються осями симетрії.Приклади завдань з ЄДІ
Вони використовуються в частині, тобто там, де потрібно виконати розгорнуте рішення завдання. Просто вибрати відповідь тут не вдасться. Тому доведеться знати формули і вміти їх застосовувати в різних ситуаціях.Перша група завдань. В ній відома довжина діагоналі куба. Потрібно обчислити його об'єм або дізнатися площа поверхні. Приміром, відома величина може дорівнювати одиниці. Тоді, щоб дізнатися обсяг і площа, потрібно скористатися формулами № 1 і 3. Але в них йде мова про ребрі, а дана діагональ. Потрібно записати ще одну формулу. Якщо подивитися на креслення куба і проведену в ньому діагональ, то можна побачити, що утворюється прямокутний трикутник. Один його катет збігається з ребром, другий - з діагоналлю межі, а гіпотенузою виявляється діагональ куба. Тоді можна записати теорему Піфагора: квадрат гіпотенузи (d 2 ) дорівнює квадрату першого катета (а 2 ), складеного з квадратом другого (а?2) 2 . Після виконання перетворень виходить, що ребро куба а так пов'язано з діагоналлю, що дорівнює d, поділеним на корінь квадратний з 3. Тепер можна початку дізнатися ребро, а потім підрахувати об'єм і площа. В конкретній задачі а=1/?3=(?3)/3. Тоді обсяг виходить рівним (?3)/9. Площа ж — два.

Читайте також

Поради
Як використовувати самогонний апарат з теном

Своїми руками
Хитрі задачки. Діагональ судоку
НАУКА
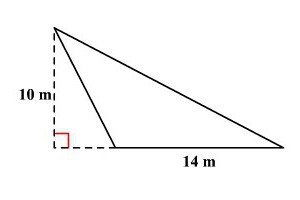
Як обчислити площу трикутника
НАУКА
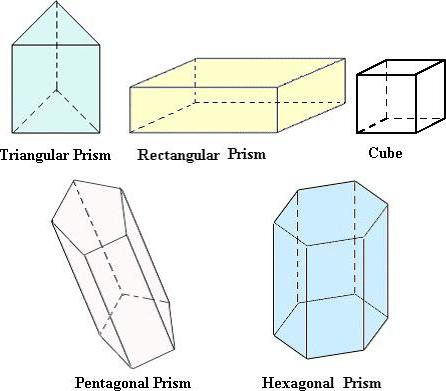
Як розрахувати обсяг різних геометричних тіл?
НАУКА
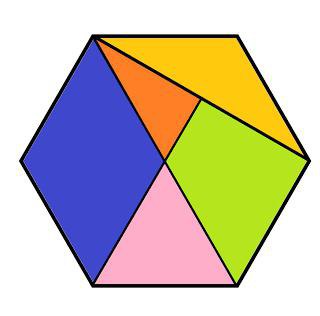
Як дізнатися площу багатокутника?
НАУКА
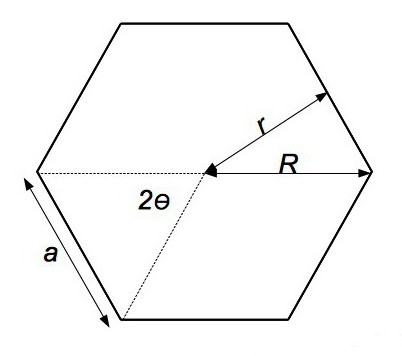
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
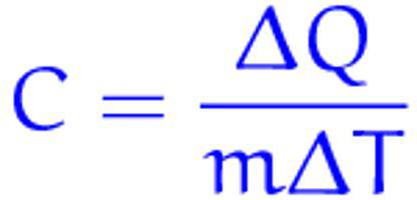
НАУКА
Питома теплоємність: для чого вона потрібна і в чому її сенс?

Дім
Вага куба бетону: види, способи вимірювання
