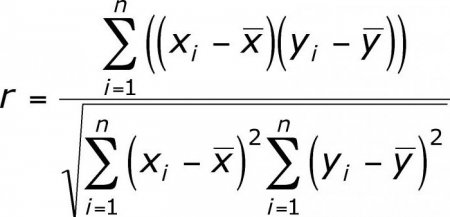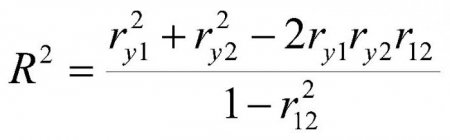Коефіцієнт кореляції і причинно-наслідковий зв'язок: формули і їх інтерпретація

Коефіцієнт кореляції – це ступінь зв'язку між двома змінними. Його розрахунок дає уявлення про те, чи є залежність між двома масивами даних. На відміну від регресії, кореляція не дозволяє пророкувати значення величин. Однак розрахунок коефіцієнта є важливим етапом попереднього статистичного аналізу. Наприклад, ми встановили, що коефіцієнт кореляції між рівнем прямих іноземних інвестицій і темпом зростання ВВП є високим. Це дає нам уявлення про те, що для забезпечення добробуту потрібно створити сприятливий клімат для зарубіжних підприємців. Не такий вже і очевидний висновок на перший погляд!

Кореляція і причинність

Мабуть, немає жодної сфери статистики, яка б так міцно увійшла в наше життя. Коефіцієнт кореляції використовується у всіх сферах суспільних знань. Головна його небезпека полягає в тому, що часто його високими значеннями спекулюють для того, щоб переконати людей і змусити їх повірити в якісь висновки. Однак насправді сильна кореляція аж ніяк не свідчить про причинно-наслідкової залежності між величинами.

Коефіцієнт кореляції: формула Пірсона і Спирмана

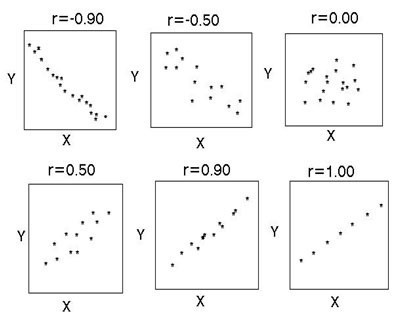
Існує кілька основних показників, які характеризують зв'язок між двома змінними. Історично першим є коефіцієнт лінійної кореляції Пірсона. Його проходять ще в школі. Він був розроблений К. Пірсоном та Дж. Юлом на основі робіт Фр. Гальтона. Цей коефіцієнт дозволяє побачити взаємозв'язок між раціональними числами, які змінюються раціонально. Він завжди більше -1 і менше 1. Негативно число свідчить про обернено пропорційній залежності. Якщо коефіцієнт дорівнює нулю, то зв'язку між змінними немає. Дорівнює позитивному числу – має місце прямо пропорційна залежність між досліджуваними величинами. Коефіцієнт рангової кореляції Спирмана дозволяє спростити розрахунки за рахунок побудови ієрархії значень змінних.

Відносини між змінними

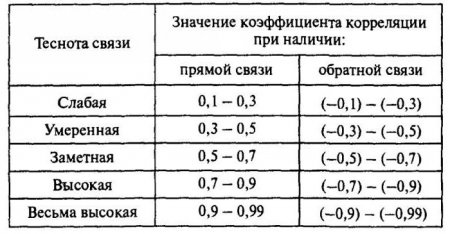
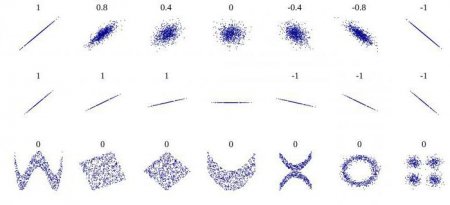
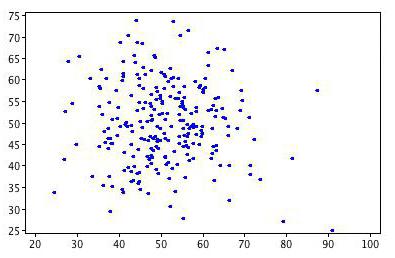
Кореляція допомагає знайти відповідь на два питання. По-перше, чи є зв'язок між змінними позитивною або негативною. По-друге, наскільки сильна залежність. Кореляційний аналіз є потужним інструментом, за допомогою якого можна отримати цю важливу інформацію. Легко побачити, що сімейні доходи і витрати падають і зростають пропорційно. Така зв'язок вважається позитивною. Навпаки, при зростанні ціни на товар, попит на нього падає. Такий зв'язок називають негативною. Значення коефіцієнта кореляції знаходяться в межах між -1 та 1. Нуль означає, що залежності між досліджуваними величинами немає. Чим ближче одержаний показник до крайнім значенням, тим сильніший зв'язок (негативна чи позитивна). Про відсутність залежності свідчить коефіцієнт від -01 до 01. Потрібно розуміти, що таке значення свідчить тільки про відсутність лінійного зв'язку.

Особливості застосування

Використання обох показників пов'язане з певними допущеннями. По-перше, наявність сильного зв'язку, не зумовлює того факту, що одна величина визначає іншу. Цілком може існувати третя величина, яка визначає кожну з них. По-друге, високий коефіцієнт кореляції Пірсона не свідчить про причинно-наслідкового зв'язку між досліджуваними змінними. По-третє, він показує виключно лінійну залежність. Кореляція може використовуватися для оцінки значущих кількісних даних (наприклад, атмосферного тиску, температури повітря), а не таких категорій, як підлогу або улюблений колір.

Множинний коефіцієнт кореляції

Пірсон і Спирман досліджували зв'язок між двома змінними. Але як діяти в тому разі, якщо їх три або навіть більше. Тут на допомогу приходить множинний коефіцієнт кореляції. Наприклад, валовий національний продукт впливають не тільки прямі іноземні інвестиції, але і монетарна і фіскальна політика держави, а також рівень експорту. Темп зростання і обсяг ВВП – це результат взаємодії цілої низки чинників. Однак потрібно розуміти, що модель множинної кореляції ґрунтується на цілому ряді спрощень та допущень. По-перше, виключається мультиколінеарності між величинами. По-друге, зв'язок між залежною і чинять на неї вплив змінними вважається лінійною.

Області використання кореляційно-регресійного аналізу

Даний метод знаходження взаємозв'язку між величинами широко застосовується в статистиці. До нього найчастіше вдаються в трьох основних випадках:

Для тестування причинно-наслідкових зв'язків між значеннями двох змінних. В результаті дослідник сподівається виявити лінійну залежність і вивести формулу, яка описує ці відносини між величинами. Одиниці їх вимірювання можуть бути різними.

Для перевірки наявності зв'язку між величинами. В цьому випадку ніхто не визначає, яка змінна є залежною. Може виявитися, що значення обох величин обумовлює якийсь інший фактор.

Для виведення рівняння. У цьому випадку можна просто підставити в нього числа та дізнатися значення невідомої змінної.

Людина в пошуках причинно-наслідкового зв'язку

Свідомість влаштовано таким чином, що нам обов'язково потрібно пояснити події, які відбуваються навколо. Людина завжди шукає зв'язок між картиною світу, в якому він живе, і отримуваною інформацією. Часто мозок створює порядок із хаосу. Він запросто може побачити причинно-наслідковий зв'язок там, де її немає. Вченим доводиться спеціально вчитися долати цю тенденцію. Здатність оцінювати зв'язки між даними об'єктивно необхідна в академічній кар'єрі.

Упередженість засобів масової інформації

Розглянемо, як наявність кореляційного зв'язку може бути неправильно витлумачено. Групу британських студентів, що відрізняються поганим поведінкою, опитали щодо того, палять їхні батьки. Потім тест опублікували в газеті. Результат показав сильну кореляцію між курінням батьків і правопорушеннями їх дітей. Професор, який проводив це дослідження, навіть запропонував помістити на пачки сигарет попередження про це. Однак існує цілий ряд проблем з таким висновком. По-перше, кореляція показує, яка з величин є незалежною. Тому цілком можна припустити, що згубна звичка батьків викликана непослухом дітей. По-друге, не можна з упевненістю сказати, що обидві проблеми не з'явилися з-за якогось третього фактора. Наприклад, низького доходу сімей. Слід зазначити емоційний аспект первинних висновків професора, який проводив дослідження. Він був затятим противником куріння. Тому немає нічого дивного в тому, що він інтерпретував результати свого дослідження саме так.

Висновки

Неправильне тлумачення кореляції як причинно-наслідкового зв'язку між двома змінними може стати причиною ганебних помилок у дослідженнях. Проблема полягає в тому, що воно лежить в основі людської свідомості. Багато маркетингові трюки побудовані саме на цій особливості. Розуміння відмінності між причинно-наслідковим зв'язком і кореляцією дозволяє раціонально аналізувати інформацію як у повсякденному житті, так і в професійній кар'єрі.