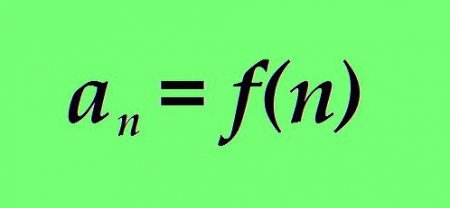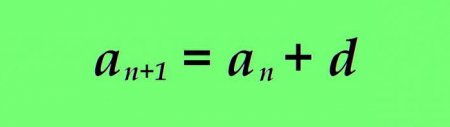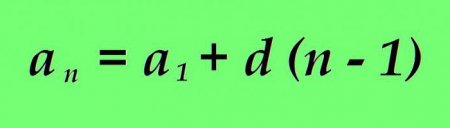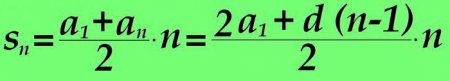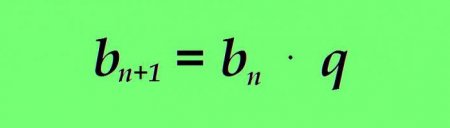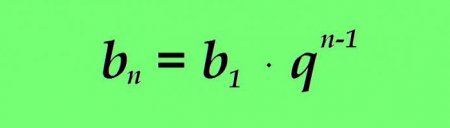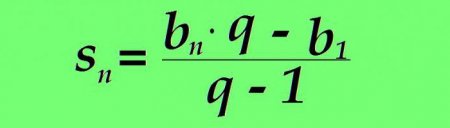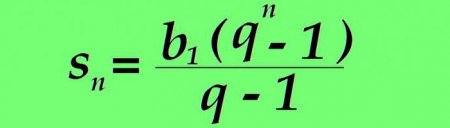Арифметична прогресія – числова послідовність
Хто-то до слова «прогресія» відноситься насторожено, як до дуже складного терміну з розділів вищої математики. А між тим сама проста арифметична прогресія – робота лічильника таксі (де вони ще залишилися). І зрозуміти суть (а у математиці немає нічого важливіше, ніж «зрозуміти суть») арифметичної послідовності не так складно, розібравши кілька елементарних понять.
де: a – значення члена числової послідовності; n – його порядковий номер; f(n) – функція, де порядковий номер у числовій послідовності n є аргументом.
номер члена – n
1
2
3
4
5
6
значення члена - a n
5
8
11
14
17
20
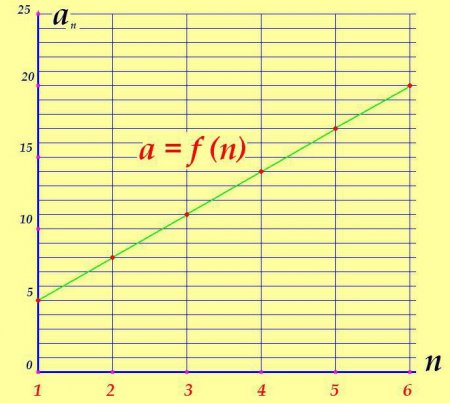
На наведеному нижче графіку неважко простежити, чому числова послідовність отримала назву «зростаюча». У випадках, коли різниця негативна (d <0), каждий последующий член по понятним причинам будет меньше предидущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убивающей.
Формула універсальна для зростаючої та спадної прогресії.
Посадка в таксі (в яку входить 3 км пробігу) коштує 50 рублів. Кожен наступний кілометр оплачується з розрахунку 22 руб./км. Відстань поїздки 30 км. Розрахувати вартість поїздки. 1. Відкинемо перші 3 км, ціна яких включена в вартість посадки. 30 – 3 = 27 км. 2. Подальший розрахунок – не що інше як розбір арифметичного числового ряду. Номер члена – число км пробігу (мінус перші три). Значення члена – сума. Перший член у даній задачі буде дорівнює a 1 = 50 р. Різниця прогресії d = 22 р. нас цікавить число – значення (27+1)-ого члена арифметичної прогресії – покази лічильника в кінці 27-го кілометра – 27999 = 28 км. a 28 = 50 + 22 • (28 - 1) = 644 На формулах, що описують ті чи інші числові послідовності, побудовані розрахунки календарних даних на як завгодно тривалий період. В астрономії в геометричній залежності від відстані небесного тіла до світила знаходиться довжина орбіти. Крім того, різні числові ряди з успіхом застосовуються в статистиці та інших прикладних розділах математики.
Математична числова послідовність
Числовою послідовністю прийнято іменувати який-небудь ряд чисел, кожне з яких має свій номер. а 1 – перший член послідовності; а 2 – другий член послідовності; а 7 – сьомий член послідовності; а n – n-й член послідовності; Однак не будь-який довільний набір цифр і чисел цікавить нас. Нашу увагу зосередимо на числової послідовності, у якій значення n-ного члена пов'язано з його порядковим номером залежністю, яку можна чітко сформулювати математично. Іншими словами: чисельне значення n-ного номера є якою-небудь функцією від n.де: a – значення члена числової послідовності; n – його порядковий номер; f(n) – функція, де порядковий номер у числовій послідовності n є аргументом.
Визначення
Арифметичною прогресією прийнято іменувати числову послідовність, в якій кожний наступний член більший (менший) попереднього на одне і те ж число. Формула n-ного члена арифметичної послідовності виглядає наступним чином: де a n – значення поточного члена арифметичної прогресії; a n+1 – формула наступного числа; d – різниця (певне число). Неважко визначити, що якщо різниця позитивна (d>0), то кожен наступний член даного ряду буде більше попереднього і така арифметична прогресія буде зростаючою. Приклад: a 1 = 5 d = 3 тодіномер члена – n
1
2
3
4
5
6
значення члена - a n
5
8
11
14
17
20
На наведеному нижче графіку неважко простежити, чому числова послідовність отримала назву «зростаюча». У випадках, коли різниця негативна (d <0), каждий последующий член по понятним причинам будет меньше предидущего, график прогрессии станет «уходить» вниз, арифметическая прогрессия, соответственно, будет именоваться убивающей.
Значення заданого члена
Іноді буває необхідно визначити значення будь-якого довільного члена a n арифметичній прогресії. Можна зробити це шляхом розрахунку послідовно значень всіх членів арифметичної прогресії, починаючи з першого до шуканого. Однак такий шлях не завжди прийнятний, якщо, наприклад, необхідно відшукати значення п'ятитисячного або восьмимільйонного члена. Традиційний розрахунок сильно затягнеться у часі. Однак конкретна арифметична прогресія може бути досліджено за допомогою певних формул. Існує формула n-ного члена: значення будь-якого члена арифметичної прогресії може бути визначено як сума першого члена прогресії з різницею прогресії, помноженої на номер шуканого члена, зменшений на одиницю.Формула універсальна для зростаючої та спадної прогресії.
Приклад розрахунку значення заданого члена
Розв'яжемо наступну задачу на знаходження значення n-ного члена арифметичної прогресії. Умова: є арифметична прогресія з параметрами: - перший член послідовності дорівнює 3; - різниця числового ряду дорівнює 12. Завдання: необхідно відшукати значення 214 члена Рішення: для визначення значення заданого члена скористаємося формулою: а(n) = a1 + d(n-1) Підставивши у вираз дані з умови задачі маємо: а(214) = a1 + d(n-1) а(214) = 3 + 12 (214-1) = 2586 Відповідь: 214-ий член послідовності рава 2586. Переваги такого способу розрахунку очевидні – всі рішення займає не більше 2 рядків.Сума заданого числа членів
Дуже часто в заданому арифметичне ряду потрібно визначити суму значень деякого його відрізку. Для цього також немає необхідності обчислювати значення кожного члена і потім підсумовувати. Такий спосіб застосовується, якщо число членів, суму яких необхідно знайти, невелика. В інших випадках зручніше скористатися наступною формулою. Сума членів арифметичної прогресії (від 1 до n дорівнює сумі першого і n-ного членів, помноженої на номер члена n та поділений надвоє. Якщо у формулі значення n-ного члена замінити на вираз з попереднього пункту статті, отримаємо:Приклад розрахунку
Для прикладу розв'яжемо задачу з наступними умовами: - перший член послідовності дорівнює нулю; - різниця дорівнює 05. В задачі потрібно визначити суму членів ряду з 56-го по 101. Рішення. Скористаємося формулою визначення суми прогресії: s(n) = (2•a1 + d•(n-1))•n/2 Спочатку визначимо суму значень 101 члена прогресії, підставивши у формулу дані умови нашої задачі: s 101 = (2•0 + 05•(101-1))•101/2 = 2525 Очевидно, для того, щоб дізнатися суму членів прогресії з 56-го по 101-й, необхідно від S 101 забрати S 55 . s 55 = (2•0 + 05•(55-1))•55/2 = 7425 Таким чином сума арифметичної прогресії для даного прикладу: s 101 - s 55 = 2525 – 7425 = 17825Приклад практичного застосування арифметичної прогресії
В кінці статті повернемося до прикладу арифметичної послідовності, наведеним у першому абзаці – таксометр (лічильник автомобіля таксі). Розглянемо такий приклад.Посадка в таксі (в яку входить 3 км пробігу) коштує 50 рублів. Кожен наступний кілометр оплачується з розрахунку 22 руб./км. Відстань поїздки 30 км. Розрахувати вартість поїздки. 1. Відкинемо перші 3 км, ціна яких включена в вартість посадки. 30 – 3 = 27 км. 2. Подальший розрахунок – не що інше як розбір арифметичного числового ряду. Номер члена – число км пробігу (мінус перші три). Значення члена – сума. Перший член у даній задачі буде дорівнює a 1 = 50 р. Різниця прогресії d = 22 р. нас цікавить число – значення (27+1)-ого члена арифметичної прогресії – покази лічильника в кінці 27-го кілометра – 27999 = 28 км. a 28 = 50 + 22 • (28 - 1) = 644 На формулах, що описують ті чи інші числові послідовності, побудовані розрахунки календарних даних на як завгодно тривалий період. В астрономії в геометричній залежності від відстані небесного тіла до світила знаходиться довжина орбіти. Крім того, різні числові ряди з успіхом застосовуються в статистиці та інших прикладних розділах математики.
Інший вид числової послідовності - геометрична
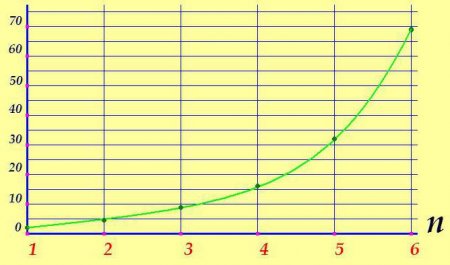
Геометрична прогресія характеризується більшими, порівняно з арифметичної, темпами зміни. Не випадково в політиці, соціології, медицині часто, щоб показати велику швидкість поширення того чи іншого явища, наприклад захворювання при епідемії, кажуть, що процес розвивається в геометричній прогресії. N-ий член геометричного числового ряду відрізняється від попереднього тим, що він множиться на яке-небудь постійне число – знаменник, наприклад, перший член дорівнює 1 знаменник відповідно дорівнює 2 тоді: n=1: 1 • 2 = 2 n=2: 2 • 2 = 4 n=3: 4 • 2 = 8 n=4: 8 • 2 = 16 n=5: 16 • 2 = 32 n=6: 32 • 2 = 64 і так далі де: b n – значення поточного члена геометричної прогресії; b n+1 – формула наступного члена геометричної прогресії; q – знаменник геометричної прогресії (постійне число). Якщо графік арифметичної прогресії являє собою пряму, то геометрична малює іншу картину: Як і у випадку з арифметичної геометрична прогресія має формулу значення довільного члена. Який-небудь n-ий член геометричної прогресії дорівнює добутку першого члена на знаменник прогресії в ступені n зменшеного на одиницю: Приклад. Маємо геометричну прогресію з першим членом рівним 3 і знаменником прогресії, рівним 15. Знайдемо 5-й член прогресії b 5 = b 1 • q (5-1) = 3 • 15 4 = 151875 Сума заданого числа членів розраховується так само за допомогою спеціальної формули. Сума n перших членів геометричної прогресії дорівнює різниці твору n - ного члена прогресії на його знаменник і першого члена прогресії, діленої на зменшений на одиницю знаменник: Якщо b n замінити користуючись розглянутим вище формулою, значення суми n перших членів розглянутого числового ряду прийме вигляд: Приклад. Геометрична прогресія починається з першого члена, рівної 1. Знаменник задано рівним 3. Знайдемо суму перших восьми членів. s8 = 1 • (3 8 -1) /(3-1) = 3280Читайте також

НАУКА
Хто такий опонент? Значення слова "опонент"

НАУКА
2:22 на годиннику: значення однакових цифр

НАУКА
Статеві органи дельфінів: опис

Техніка
Як дізнатися номер свого номера "Київстар"? Всі способи

НАУКА
Як обчислити межі послідовностей?
НАУКА
Як знайти корінь рівняння: лінійного, квадратного, кубічного?

НАУКА
Англійське вимова слів: як побудувати процес опрацювання навички?

НАУКА
На які питання відповідає доповнення? Теорія, приклади