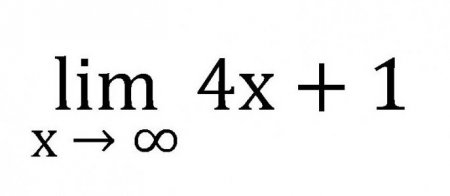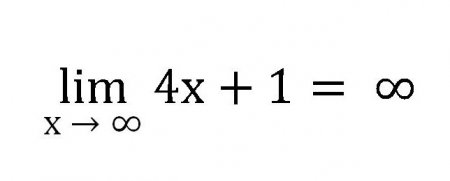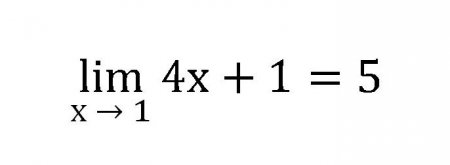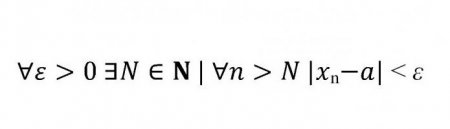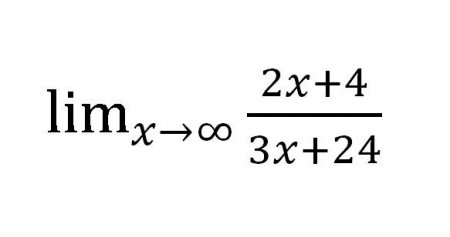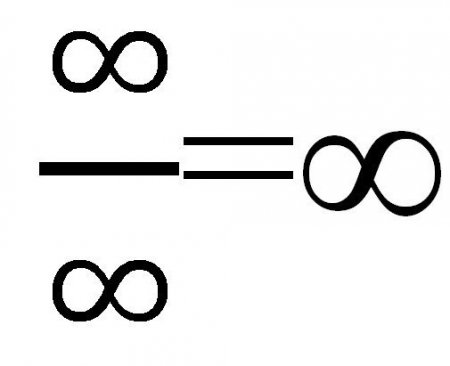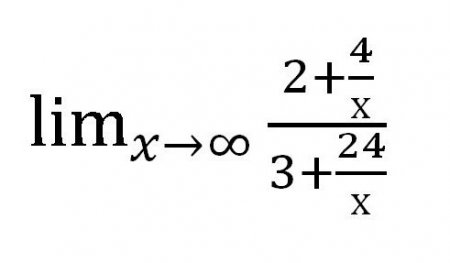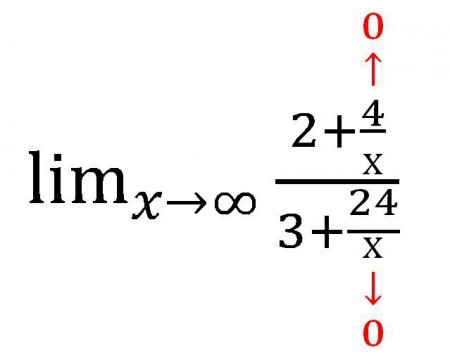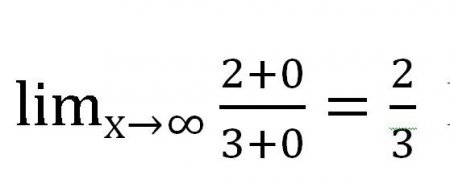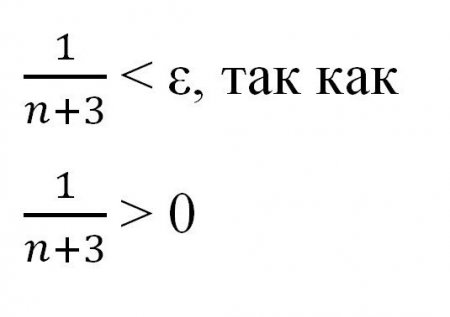Як обчислити межі послідовностей?
Математика — наука, яка будує світ. Як учений, так і простий чоловік — ніхто не зможе обійтися без неї. Спочатку маленьких дітей вчать рахувати, потім складати, віднімати, множити і ділити, до середньої школи в хід вступають літерні позначення, а в старшій без них вже не обійтися. Але сьогодні мова піде про те, на чому будується вся відома математика. Про співтоваристві чисел під назвою «межі послідовностей».
Слово «межа» також легко трактується — це кінець чого-небудь. Однак в математиці межі послідовностей — це такі значення на числовій прямій, до яких прагне послідовність чисел. Чому прагне, а не закінчується? Все просто, у числовій прямій немає кінця, а більшість послідовностей, як промені, мають тільки початок і виглядають наступним чином: х 1 , х 2 , х 3 , х n Звідси визначення послідовності — функція натурального аргументу. Більш простими словами — це ряд членів деякого безлічі.
Завдання: «Нехай а 1 =15 а крок прогресії числового ряду d=4. Побудуйте перші 4 члена цього ряду» Рішення: а 1 = 15 (по умові) — перший член прогресії (числового ряду). а 2 = 15+4=19 — другий член прогресії. а 3 =19+4=23 — третій член. а 4 =23+4=27 — четвертий член. Однак подібним методом важко дістатися до великих значень, наприклад до а 125. . Спеціально для таких випадків була виведена зручна для практики формула: а n =a 1 +d(n–1). У даному разі а 125 =15+4(125-1)=511.
Всі межі позначаються скорочено lim. Запис межі складається з скорочення lim, будь-якої змінної, прагне до певного числа, нулю або нескінченності, а також із самої функції. Легко зрозуміти, що визначення межі послідовності може бути сформульовано наступним чином: це деяке число, до якого нескінченно наближаються всі члени послідовності. Простий приклад: а x = 4x+1. Тоді сама послідовність буде виглядати наступним чином. 5913 1721x Таким чином, дана послідовність нескінченно збільшуватися, а, значить, її межа дорівнює нескінченності при x->?, і записувати це слід так: Якщо ж взяти схожу послідовність, але буде прагнути до 1 то отримаємо: a x = 4x + 1. А ряд чисел буде таким: 141.846 4944 і т. д. Кожен раз потрібно підставляти число все більше приближеннее до одиниці (010.209 0986). З цього ряду видно, що межа функції — це п'ять.
З цієї частини варто запам'ятати, що таке границя числової послідовності, визначення і метод вирішення простих завдань. Єдиність границі послідовності. Межа у будь-якій послідовності може бути тільки один або не бути зовсім. Той же приклад з чергою, в якій може бути тільки один кінець. Якщо ряд чисел має межу, то послідовність цих чисел обмежена. Межа суми (різниці, добутку) послідовностей дорівнює сумі (різниці, добутку) їх меж. Межа приватного від ділення двох послідовностей дорівнює приватному меж тоді і тільки тоді, коли знаменник не звертається в нуль. 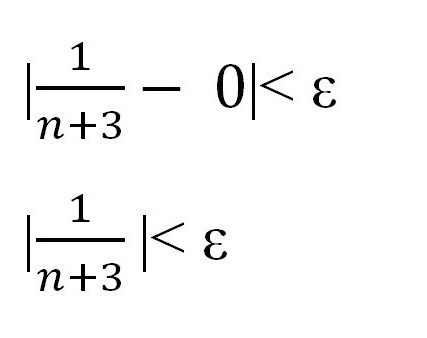 Виразимо через n «епсилон», щоб показати існування якогось номери і довести наявність межі послідовності. На цьому етапі важливо нагадати, що «епсилон» і «ен» - числа позитивні і не дорівнюють нулю. Тепер можна продовжувати подальші перетворення, використовуючи знання про нерівностях, отримані в середній школі. Звідки виходить, що n > -3 + 1/?. Оскільки варто пам'ятати, що мова йде про натуральних числах, то результат можна округлити, занісши його в квадратні дужки. Таким чином, було доведено, що для будь-якого значення околиці «епсилон» точки а=0 знайшлося значення таке, що виконується початкова нерівність. Звідси можна сміливо стверджувати, що число а є межа заданій послідовності. Що і потрібно було довести. Ось таким зручним методом можна довести границя числової послідовності, якою б складною вона на перший погляд не була. Головне — не впадати в паніку при вигляді завдання.
Виразимо через n «епсилон», щоб показати існування якогось номери і довести наявність межі послідовності. На цьому етапі важливо нагадати, що «епсилон» і «ен» - числа позитивні і не дорівнюють нулю. Тепер можна продовжувати подальші перетворення, використовуючи знання про нерівностях, отримані в середній школі. Звідки виходить, що n > -3 + 1/?. Оскільки варто пам'ятати, що мова йде про натуральних числах, то результат можна округлити, занісши його в квадратні дужки. Таким чином, було доведено, що для будь-якого значення околиці «епсилон» точки а=0 знайшлося значення таке, що виконується початкова нерівність. Звідси можна сміливо стверджувати, що число а є межа заданій послідовності. Що і потрібно було довести. Ось таким зручним методом можна довести границя числової послідовності, якою б складною вона на перший погляд не була. Головне — не впадати в паніку при вигляді завдання. Сума будь-якої кількості скільки завгодно малих величин буде також малою величиною. Сума будь-якої кількості великих величин буде нескінченно великою величиною. Твір як завгодно малих величин нескінченно мало. Твір скільки завгодно великих чисел — величина нескінченно велика. Якщо вихідна послідовність прагне до нескінченно великого числа, то величина, зворотна їй, буде нескінченно малої і прагнути до нуля. Насправді обчислити межа послідовності - не така складна задача, якщо знати простий алгоритм. Але межі послідовностей — тема, що вимагає максимуму уваги і посидючості. Звичайно, досить просто вловити суть рішення подібних виразів. Починаючи з малого, з часом можна досягти великих вершин.
Що таке послідовності і де та межа?
Значення слова «послідовність» трактувати неважко. Це така побудова речей, де хтось або щось розташовані в певному порядку черги. Наприклад, черга за квитками в зоопарк — це послідовність. Причому вона може бути тільки одна! Якщо, наприклад, подивитися на чергу в магазин — це одна послідовність. А якщо одна людина з цієї черги раптом піде, то це вже інша чергу, інший порядок.Слово «межа» також легко трактується — це кінець чого-небудь. Однак в математиці межі послідовностей — це такі значення на числовій прямій, до яких прагне послідовність чисел. Чому прагне, а не закінчується? Все просто, у числовій прямій немає кінця, а більшість послідовностей, як промені, мають тільки початок і виглядають наступним чином: х 1 , х 2 , х 3 , х n Звідси визначення послідовності — функція натурального аргументу. Більш простими словами — це ряд членів деякого безлічі.
Як будується числова послідовність?
Найпростіший приклад числової послідовності може виглядати так: 123 4 n У більшості випадків для практичних цілей послідовності будуються з цифр, причому кожен наступний член ряду, позначимо його Х, має своє ім'я. Наприклад: х 1 — перший член послідовності; х 2 — другий член послідовності; х 3 — третій член; х n — енний член. В практичних методах послідовність задається загальною формулою, в якій є деяка змінна. Наприклад: Х n =3n, тоді сам ряд чисел буде виглядати так: х 1 = 3; х 2 = 6; х 3 = 9; і т. д. Варто не забувати, що при загальній запису послідовностей можна використовувати будь-латинські букви, а не тільки Х. Наприклад: y, z, k і т. д.Арифметична прогресія як частина послідовностей
Перш ніж шукати межі послідовностей, доцільно глибше зануритися в саме поняття такого числового ряду, з яким стикалися, будучи в середніх класах. Арифметична прогресія — це ряд чисел, в якому різниця між сусідніми членами постійна.Завдання: «Нехай а 1 =15 а крок прогресії числового ряду d=4. Побудуйте перші 4 члена цього ряду» Рішення: а 1 = 15 (по умові) — перший член прогресії (числового ряду). а 2 = 15+4=19 — другий член прогресії. а 3 =19+4=23 — третій член. а 4 =23+4=27 — четвертий член. Однак подібним методом важко дістатися до великих значень, наприклад до а 125. . Спеціально для таких випадків була виведена зручна для практики формула: а n =a 1 +d(n–1). У даному разі а 125 =15+4(125-1)=511.
Види послідовностей
Більшість послідовностей нескінченні, це варто запам'ятати на все життя. Існує два цікавих виду числового ряду. Перший задається формулою а n =(-1) n . Математики часто називають цю послідовностей мигалкою. Чому? Перевіримо її числовий ряд. -1 1 -1 , 1 -1 1 і т. д. На такому прикладі стає ясно, що числа в послідовності можуть легко повторюватися. Факториальная послідовність. Легко здогадатися — у формулі, задає послідовність, присутній факторіал. Наприклад: а n = (n+1)! Тоді послідовність буде виглядати наступним чином: а 1 = 1х2=2; а 2 = 1х2х3 = 6; а 3 = 1х2х3х4 =24 і т. д. Послідовність, задана арифметичною прогресією називається нескінченно спадної, якщо для всіх її членів дотримується нерівність -1 n = (-1/2) n . а 1 = – 1/2 ; R3r3r3491. а 2 = 1/4 ; R3r3r3491. а 3 = – 1/8 і т. д. Існує навіть послідовність, що складається з одного і того ж числа. Так, а n =6 складається з нескінченного безлічі шісток.Визначення межі послідовності
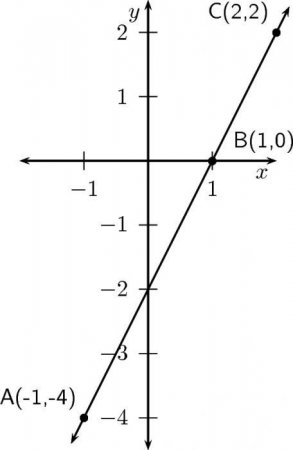
Межі послідовностей давно існують в математиці. Звичайно, вони заслужили своє власне грамотне оформлення. Отже, час дізнатися визначення меж послідовностей. Для початку розглянемо докладно межа для лінійної функції:З цієї частини варто запам'ятати, що таке границя числової послідовності, визначення і метод вирішення простих завдань.
Загальне позначення межі послідовностей
Розібравши границя числової послідовності, визначення і приклади, можна приступити до більш складної теми. Абсолютно всі межі послідовностей можна сформулювати однією формулою, яку зазвичай розбирають у першому семестрі. Отже, що ж означає цей набір букв, модулів і знаків нерівностей? ? — квантор загальності, замінює фрази «для всіх», «для всього» і т. п. ? — квантор існування, у даному випадку означає, що існує деяке значення N, що належить множині натуральних чисел. Довга вертикальна паличка, наступна за N, означає, що дане безліч N «таке, що». На практиці вона може означати «такий, що», «такі, що» і т. п. Далі йде модуль. Очевидно, модуль — це відстань, яка за визначенням не може бути від'ємним. Значить модуль різниці строго менше "епсилона". Для закріплення матеріалу прочитайте формулу вголос.Невизначеність і визначеність межі
Метод знаходження межі послідовностей, який розглядалося вище, нехай і простий у застосуванні, але не так раціональний на практиці. Спробуйте знайти межу ось такий функції: Якщо підставляти різні значення «ікс» (з кожним разом збільшуються: 101001000 і т. д.), то в чисельнику отримаємо ?, але в знаменнику теж ?. Виходить досить дивна дріб: Але чи так це насправді? Обчислити границю числової послідовності в даному випадку здається досить легко. Можна було б залишити все, як є, адже відповідь готовий, і він отриманий на розумних умовах, однак є ще один спосіб спеціально для таких випадків. Для початку знайдемо старшу ступінь в чисельнику дробу — це 1 т. к. х можна представити як х 1 . Тепер знайдемо старшу ступінь в знаменнику. Теж 1. Розділимо і чисельник, і знаменник на змінну у вищій ступеня. В цьому випадку дріб ділимо на х 1 . Далі знайдемо, до якого значенню прагне кожен доданок, що містить змінну. В даному випадку розглядаються дробу. При х->? значення кожного з дробів прагне до нуля. При оформленні роботи в писменном вигляді варто зробити такі виноски: Виходить наступне вираз: Звичайно ж, дробу, що містять х, не стали нулями! Але їх значення настільки мало, що цілком дозволено не враховувати його при розрахунках. Насправді ж х ніколи не буде дорівнює 0 в даному випадку, адже на нуль ділити не можна.Що таке околиця?
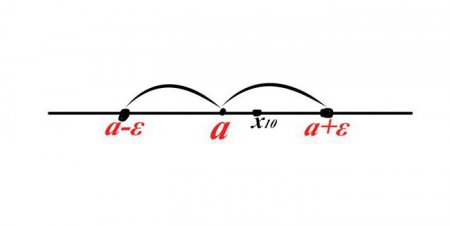
Припустимо, у розпорядженні професора складна послідовність, задана, очевидно, не менш складною формулою. Професор знайшов відповідь, але підходить він? Адже всі люди помиляються. Огюст Коші свого часу придумав відмінний спосіб докази меж послідовностей. Його спосіб назвали оперування околицями. Припустимо, що існує деяка точка а, її околиця в обидві сторони на числової прямої дорівнює ? («epsilon»). Оскільки остання змінна — відстань, то її значення завжди позитивно. Тепер задамо деяку послідовність х n покладемо, що десятий член послідовності (x 10 ) входить в околицю а. Як записати цей факт на математичному мові? Припустимо, х 10 знаходиться правіше від точки а, тоді відстань х 10 –а <Оµ, однако, если расположить «икс десятое» левее точки а, то расстояние получится отрицательним, а ето невозможно, значит, следует занести левую часть неравенства под модуль. Получится |х 10 –а| 0 причому вся околиця має свій натуральний номер N, такий, що всі члени послідовності з більш значними номерами опиняться всередині послідовності |x n – a| < Оµ. З такими знаннями легко здійснити рішення меж послідовності, довести або спростувати готову відповідь.Теореми
Теореми про границі послідовностей — важлива складова теорії, без якої неможлива практика. Є лише чотири головних теореми, запам'ятавши які, можна в рази полегшити хід рішення або докази:Доказ послідовностей
Іноді потрібно вирішити зворотну задачу, довести заданий межа числової послідовності. Розглянемо на прикладі. Довести, що межа послідовності, заданої формулою, дорівнює нулю. З розглянутого вище правилом, для будь-якої послідовності повинно виконуватися нерівність |x n – a| <Оµ. Подставим заданное значение и точку отсчёта. Получим: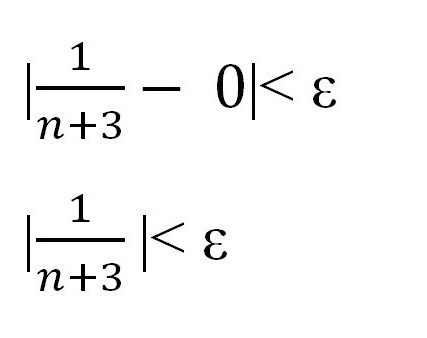
А може, його немає?
Існування границі послідовності необов'язково на практиці. Легко можна зустріти такі ряди чисел, які дійсно не мають кінця. Приміром, та ж «мигалка» x n = (-1) n . очевидно, що послідовність, що складається всього лише з двох цифр, що циклічно повторюються, не може мати меж. Та ж історія повторюється з послідовностями, що складаються з одного числа, дробовими, які мають в час обчислень невизначеність будь-якого порядку ( 0/0 ?/?, ?/0 і т. д.). Однак слід пам'ятати, що неправильне обчислення теж має місце бути. Іноді межа последоватей знайти допоможе повторна перевірка власного рішення.Монотонна послідовність
Вище розглядалися кілька прикладів послідовностей, методи їх вирішення, а тепер спробуємо взяти більш певний випадок і назвемо його «монотонною послідовністю». Визначення: будь-яку послідовність справедливо називати монотонно зростаючою, якщо для неї виконується строга нерівність x n x n +1. Поряд з цими двома умовами існують також подібні несуворі нерівності. Відповідно, x n = x n +1 (невозрастающая послідовність). Але легше розуміти подібне на прикладах. Послідовність, задана формулою х n = 2+n, утворює наступний ряд чисел: 456 і т. д. Це монотонно зростаюча послідовність. А якщо взяти x n =1/n, то одержимо ряд: 1/3 1/4 , 1/5 і т. д. Це монотонно спадна послідовність.Межа збіжної та обмеженої послідовності
Обмежена послідовність — послідовність, що має межу. Сходиться послідовність — ряд чисел, що має нескінченно малий межа. Таким чином, межа обмеженою послідовності — це будь-яке дійсне чи комплексне число. Пам'ятайте, що межа може бути тільки один. Межа збіжної послідовності — це величина нескінченно мала (дійсна чи комплексна). Якщо накреслити діаграму послідовності, то в певній точці вона буде як би сходитися, прагнути звернутися в певну величину. Звідси і назва — сходиться послідовність.Межа монотонної послідовності
Межа у такій послідовності може бути, а може і не бути. Спочатку корисно зрозуміти, коли він є, звідси можна відштовхнутися при доведенні відсутності межі. Серед монотонних послідовностей виділяють сходиться і розходиться. Сходиться — це така послідовність, яка утворена безліччю х і має в даному безлічі дійсний або комплексний межа. Расходящаяся — послідовність, не має межі у своєму множині (ні дійсного, ні комплексного). Причому послідовність сходиться, якщо при геометричному зображенні її верхній і нижній межі сходяться. Межа збіжної послідовності у багатьох випадках може бути дорівнює нулю, так як будь-нескінченно мала послідовність має відомий межа (нуль). Яку сходиться послідовність ні візьми, вони всі обмежені, проте далеко не всі обмежені послідовності сходяться. Сума, різниця, добуток двох збіжних послідовностей - також сходиться послідовність. Проте приватна може бути також збіжної, якщо воно визначено!Різні дії з межами
Межі послідовностей — це така ж істотна (в більшості випадків) величина, як і цифри і числа: 1215 24362 і т. д. Виходить, що з межами можна проводити певні операції. По-перше, як і цифри і числа, межі будь-яких послідовностей можна складати і віднімати. Виходячи з третьої теореми про границі послідовностей, справедливо наступне рівність: межа суми послідовностей дорівнює сумі їх меж. По-друге, виходячи з четвертої теореми про границі послідовностей, справедливо наступне рівність: межа твору n-ого кількості послідовностей дорівнює добутку їх меж. То ж справедливо і для ділення: межа приватного двох послідовностей дорівнює частці їх меж, за умови, що межа не дорівнює нулю. Адже якщо межа послідовності буде дорівнює нулю, то вийде ділення на нуль, що неможливо.Властивості величин послідовностей
Здавалося б, границя числової послідовності вже розібраний досить докладно, проте не раз згадуються такі фрази, як «нескінченно малі» і «нескінченно великі» числа. Очевидно, якщо є послідовність 1/х, де x->?, то така дріб нескінченно мала, а якщо та ж послідовність, але межа прагне до нуля (х->0), то дріб стає нескінченно великою величиною. А у таких величин є свої особливості. Властивості межі послідовності, що має які завгодно малі або великі величини, полягають у наступному:Читайте також
НАУКА
Як знайти корінь рівняння: лінійного, квадратного, кубічного?
НАУКА
Як обчислити площу трикутника
НАУКА
Проста задача: як знайти периметр?
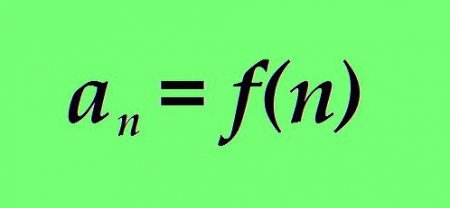
НАУКА
Арифметична прогресія – числова послідовність
НАУКА
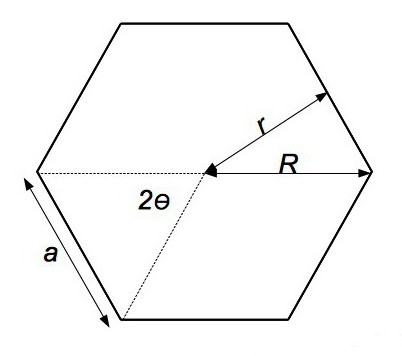
Як дізнатися площу багатокутника?
НАУКА
Що таке непарні числа і як їх впізнати?

НАУКА
Як скоротити дріб? Правила на всі ситуації

НАУКА
Градація: приклад у прозі і поезії