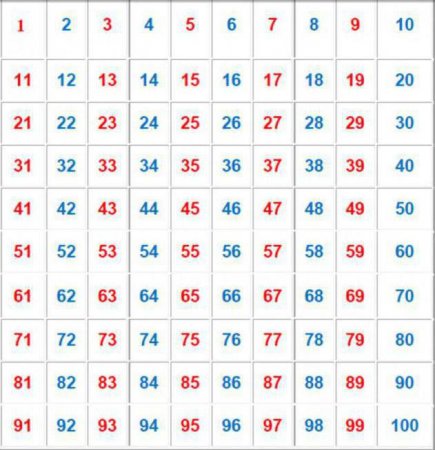
Що таке непарні числа і як їх впізнати?
Перш ніж говорити про парні і непарні числа, варто запам'ятати кілька моментів про те, які взагалі групи чисел бувають. Це необхідно для того, щоб не намагатися з'ясовувати парність дробу.
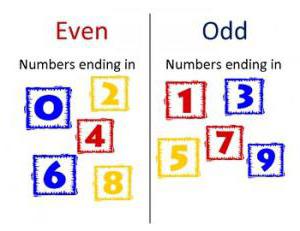 Саме для них вперше дається визначення парності. Щоб зрозуміти, яке число непарне, потрібно запам'ятати ознака парного. Воно закінчується на одну із цифр: 024 6 8. Всі інші будуть непарними. Мінімальне з них дорівнює одиниці. Максимального не існує.
Саме для них вперше дається визначення парності. Щоб зрозуміти, яке число непарне, потрібно запам'ятати ознака парного. Воно закінчується на одну із цифр: 024 6 8. Всі інші будуть непарними. Мінімальне з них дорівнює одиниці. Максимального не існує.
До речі, для них не вводиться поняття парності. Тому непарні числа, записані у вигляді дробу, не існують зовсім.
При складанні парного з непарним маємо таку запис: 2n + (2n + 1) = 4n + 1. Перший доданок — парне число, до якого додається одиниця. Останнє доданок не дасть розділити цей результат на два націло. Третя дія — множення. При його виконанні завжди буде парний відповідь, якщо є хоча б один множник парний. У ситуації, коли перемножуються два непарні числа, результатом виявиться непарне. Для ілюстрації останнього потрібно зробити такий запис: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Знову перший доданок являє собою парне число, а одиниця зробить його непарних. З четвертим дією — поділом - все не так однозначно. Почати можна з двох парних. По-перше, може вийти дріб, тоді про парності мови не йде. По-друге, результатом буває ціле число. Але і тоді однозначної відповіді на питання про майбутню парності отримати неможливо. Оцінити її можна тільки після виконання ділення. Відповідь може бути як парним, так і непарним. Якщо непарне число ділиться на парне, то відповідь завжди виявляється дробовим. Значить, його парність не визначається. Коли в розподілі беруть участь непарні числа, то результатом може виявитися дріб. Але якщо відповідь цілий, то він обов'язково буде непарною. При поділі парного на непарне, як в попередній ситуації, можливо два варіанти: дріб або ціле число. У другому випадку воно завжди буде парною.
З яких чисел починається вивчення в основній школі?
Першими йдуть натуральні. Вони також спочатку з'явилися історично. Людству необхідно підраховувати предмети. Причому при рахунку нуль не використовується, тому він не входить в групу натуральних чисел. Тут всі цілі, які більше одиниці.
Які числа йдуть далі?
Цілі. В їх безліч входить вже нуль і від'ємні числа. Ланцюжок натуральних чисел була обмежена ліворуч, а праворуч тривала нескінченно. З цілими виявляється нескінченна кількість чисел і ліворуч від нуля. У цей момент трохи змінюється визначення парності. Тепер воно повинно ділитися на два без залишку. Значить, непарні числа при діленні на два дають відповідь з залишком. Причому навіть вводиться загальна запис: для парних — 2n, непарні — (2n+1). Якщо для натуральних не існує тільки максимального парного або непарного, то у цілих немає і мінімального.А що потім?
Раціональні (інша назва - речові) числа. Крім вже згаданих, це безліч входять ще й дробу. Тобто числа, які можна подати у вигляді двох. Перше з них є чисельником і представляється у вигляді цілого числа. Друге — знаменник, який ніколи не дорівнює нулю.До речі, для них не вводиться поняття парності. Тому непарні числа, записані у вигляді дробу, не існують зовсім.

Які результати дають дії з парними і непарними числами?
Їх можна розглянути в порядку ускладнення арифметичного дії. Тоді першим і другим підуть додавання і віднімання. Неважливо, який з них виконується, відповідь буде залежати тільки від початкової пари чисел. Наприклад, якщо початкові числа парні, то результат дії буде ділитися на два. Такий самий результат буде, якщо стоїть різниця або сума непарних чисел. Щоб отримати непарне число, доведеться додавати або віднімати парне з непарною. Це легко можна перевірити, використовуючи їх загальну запис. Наприклад, додавання двох парних чисел: 2n+2n = 4n = 2*2n. Тут 2n — парне число, яке ще множиться на два. Значить, воно точно буде ділитися націло на двійку. Тобто відповідь — парний.При складанні парного з непарним маємо таку запис: 2n + (2n + 1) = 4n + 1. Перший доданок — парне число, до якого додається одиниця. Останнє доданок не дасть розділити цей результат на два націло. Третя дія — множення. При його виконанні завжди буде парний відповідь, якщо є хоча б один множник парний. У ситуації, коли перемножуються два непарні числа, результатом виявиться непарне. Для ілюстрації останнього потрібно зробити такий запис: (2n + 1) * (2n + 1) = 4n + 2n + 2n + 1 = 8n + 1. Знову перший доданок являє собою парне число, а одиниця зробить його непарних. З четвертим дією — поділом - все не так однозначно. Почати можна з двох парних. По-перше, може вийти дріб, тоді про парності мови не йде. По-друге, результатом буває ціле число. Але і тоді однозначної відповіді на питання про майбутню парності отримати неможливо. Оцінити її можна тільки після виконання ділення. Відповідь може бути як парним, так і непарним. Якщо непарне число ділиться на парне, то відповідь завжди виявляється дробовим. Значить, його парність не визначається. Коли в розподілі беруть участь непарні числа, то результатом може виявитися дріб. Але якщо відповідь цілий, то він обов'язково буде непарною. При поділі парного на непарне, як в попередній ситуації, можливо два варіанти: дріб або ціле число. У другому випадку воно завжди буде парною.
Читайте також

НАУКА
2:22 на годиннику: значення однакових цифр

Техніка
Прилад для вимірювання октанового числа бензину "Октис-2": відгуки, інструкція, принцип роботи

Компютер і інтернет
Функція Scanf C: опис

Своїми руками
Хитрі задачки. Діагональ судоку

НАУКА
Як обчислити межі послідовностей?
НАУКА
Як знайти корінь рівняння: лінійного, квадратного, кубічного?
НАУКА
Проста задача: як знайти периметр?

НАУКА
Як скоротити дріб? Правила на всі ситуації