Проста задача: як знайти периметр?
Знання про те, як знайти периметр, учні отримують ще в початковій школі. Потім ця інформація постійно використовується протягом всього курсу математики і геометрії.
Букви завжди вибирають за алфавітом. Для трикутника вони будуть першими трьома. У шестикутника їх буде 6 - від а до f. Це зручно для введення формул.
Тепер про те, як знайти периметр. Він є сумою довжин всіх сторін фігури. Кількість доданків залежить від її виду. Позначається периметр латинською літерою Р. Одиниці виміру збігаються з тими, які надані для сторін.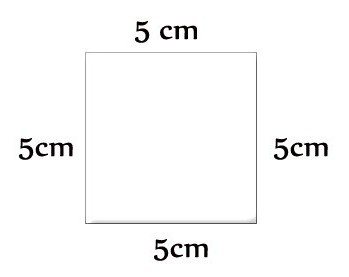
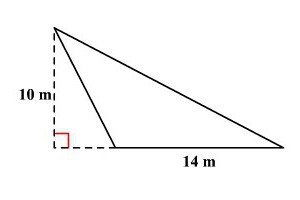
Приватним випадком зазначеної теореми є сформульована Піфагором для прямокутного трикутника. В ній значення косинуса прямого кута стає рівним нулю, а отже, останнє доданок просто зникає. Бувають ситуації, коли дізнатися, як знайти периметр трикутника, можна по одній стороні. Але при цьому відомі ще і кути фігури. Тут на допомогу приходить теорема синусів, коли відношення довжин сторін до синусам відповідних протилежних кутів рівні. У ситуації, коли периметр фігури потрібно дізнатися по площі, знадобляться інші формули. Наприклад, якщо відомий радіус вписаного кола, то в питанні про те, як знаходити периметр трикутника, стане в нагоді наступна формула: S=p*r, тут р — півпериметр. Його потрібно вивести з цієї формули і помножити на два.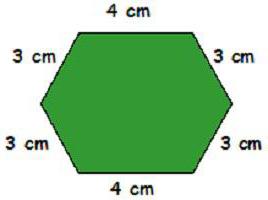
Рішення. Потрібно скористатися рівнянням, яке зазначено вище, і просто підставити в нього дані в завданні значення. Розрахунки легкі, вони призводять до числа 12 див.
Відповідь. Периметр трикутника дорівнює 12 див. Умова другий. Одна сторона трикутника дорівнює 10 див. Відомо, що друга на 2 см більше першої, а третя в 15 рази більше першою. Потрібно обчислити його периметр.
Рішення . Для того щоб дізнатися, чи потрібно порахувати дві сторони. Друга визначиться як сума 10 і 2 третя дорівнює добутку 10 і 15. Потім залишиться тільки порахувати суму трьох значень: 1012 і 15. Результатом буде 37 див.
Відповідь. Периметр дорівнює 37 див.
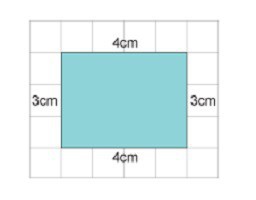
Умова третьої. Є прямокутник і квадрат. Одна сторона прямокутника дорівнює 4 см, а інша-на 3 см більше. Потрібно обчислити значення сторони квадрата, якщо його периметр менше на 6 см, ніж у прямокутника.
Рішення. Друга сторона прямокутника дорівнює 7. Знаючи це, легко обчислити його периметр. Розрахунок дає 22 див.
Щоб дізнатися сторону квадрата, потрібно спочатку відняти 6 з периметра прямокутника, а потім поділити отримане число на 4. В результаті маємо число 4.
Відповідь. Сторона квадрата 4 див.
Загальна для всіх фігур теорія
Сторони прийнято позначати латинськими літерами. Причому їх можна позначати як відрізки. Тоді букв потрібно по два для кожної сторони і записані великими. Або ввести позначення однією літерою, яка обов'язково буде маленькою.Букви завжди вибирають за алфавітом. Для трикутника вони будуть першими трьома. У шестикутника їх буде 6 - від а до f. Це зручно для введення формул.
Тепер про те, як знайти периметр. Він є сумою довжин всіх сторін фігури. Кількість доданків залежить від її виду. Позначається периметр латинською літерою Р. Одиниці виміру збігаються з тими, які надані для сторін.

Формули периметрів різних фігур
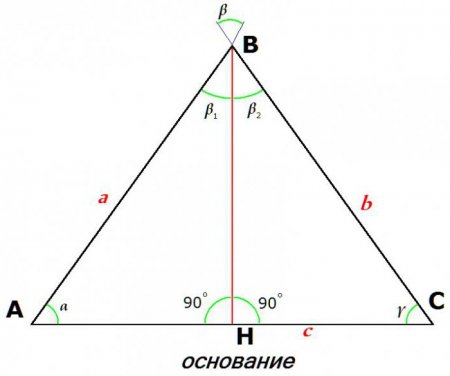
Для трикутника: Р=а+в+с. Якщо він рівнобедрений, то формула перетвориться: Р=2а+ст. Як знайти периметр трикутника, якщо він рівносторонній? Допоможе така: Р=3а. Для довільного чотирикутника: Р=а+в+с+d. Його приватним випадком є квадрат, формула периметра: Р=4а. Є ще прямокутник, тоді потрібна така рівність: Р=2(а+в).
Як бути, якщо невідома довжина однієї або декількох сторін трикутника?
Скористатися теоремою косинусів, якщо серед даних є дві сторони і кут між ними, який позначається буквою А. Тоді до того, як знайти периметр, доведеться порахувати третю сторону. Для цього знадобиться така формула: с2 = а2 + в2 — 2 ав cos(А).Приватним випадком зазначеної теореми є сформульована Піфагором для прямокутного трикутника. В ній значення косинуса прямого кута стає рівним нулю, а отже, останнє доданок просто зникає. Бувають ситуації, коли дізнатися, як знайти периметр трикутника, можна по одній стороні. Але при цьому відомі ще і кути фігури. Тут на допомогу приходить теорема синусів, коли відношення довжин сторін до синусам відповідних протилежних кутів рівні. У ситуації, коли периметр фігури потрібно дізнатися по площі, знадобляться інші формули. Наприклад, якщо відомий радіус вписаного кола, то в питанні про те, як знаходити периметр трикутника, стане в нагоді наступна формула: S=p*r, тут р — півпериметр. Його потрібно вивести з цієї формули і помножити на два.

Приклади завдань
Умова першої. Дізнатися периметр трикутника, сторони якого 3 4 і 5 див.Рішення. Потрібно скористатися рівнянням, яке зазначено вище, і просто підставити в нього дані в завданні значення. Розрахунки легкі, вони призводять до числа 12 див.
Відповідь. Периметр трикутника дорівнює 12 див. Умова другий. Одна сторона трикутника дорівнює 10 див. Відомо, що друга на 2 см більше першої, а третя в 15 рази більше першою. Потрібно обчислити його периметр.
Рішення . Для того щоб дізнатися, чи потрібно порахувати дві сторони. Друга визначиться як сума 10 і 2 третя дорівнює добутку 10 і 15. Потім залишиться тільки порахувати суму трьох значень: 1012 і 15. Результатом буде 37 див.
Відповідь. Периметр дорівнює 37 див.
Умова третьої. Є прямокутник і квадрат. Одна сторона прямокутника дорівнює 4 см, а інша-на 3 см більше. Потрібно обчислити значення сторони квадрата, якщо його периметр менше на 6 см, ніж у прямокутника.
Рішення. Друга сторона прямокутника дорівнює 7. Знаючи це, легко обчислити його периметр. Розрахунок дає 22 див.
Щоб дізнатися сторону квадрата, потрібно спочатку відняти 6 з периметра прямокутника, а потім поділити отримане число на 4. В результаті маємо число 4.
Відповідь. Сторона квадрата 4 див.
Читайте також

Дім
Як порахувати периметр кімнати для покупки оздоблювальних матеріалів

Дім
Практичні поради про те, як дізнатися площа кімнати
НАУКА
Як обчислити площу трикутника
НАУКА
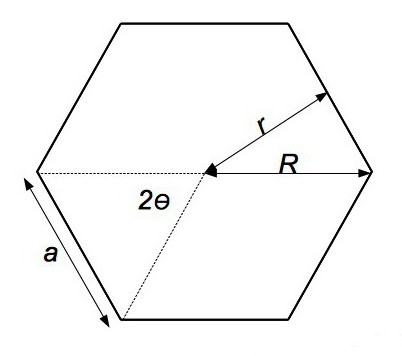
Як дізнатися площу багатокутника?
НАУКА
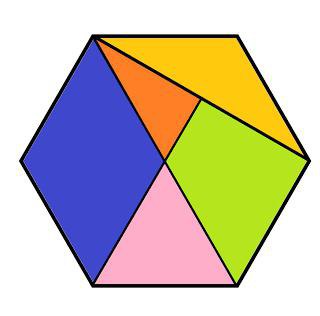
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
НАУКА
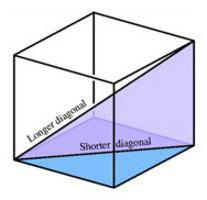
Діагональ куба: що це таке і як її знайти?
НАУКА
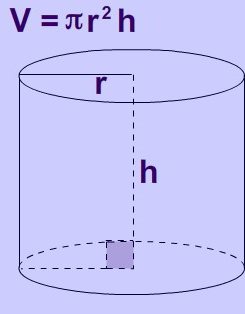
Як знайти об'єм циліндра: формули і завдання
НАУКА
Ознаки, складові елементи та властивості рівнобедреного трикутника
