Як знайти об'єм циліндра: формули і завдання
Питання, як знайти об'єм циліндра, може виникнути не тільки у школяра. Адже таку форму має, наприклад, каструля, ємність якої іноді терміново потрібно дізнатися. Ось тоді буде потрібно знання спеціальної формули.
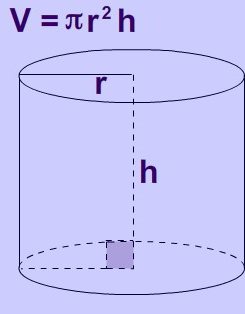 Яким би не був вигляд тіла, все одно потрібно знати про те, як знайти об'єм циліндра. Але спочатку потрібно визначитися з деякими теоретичними даними.
Яким би не був вигляд тіла, все одно потрібно знати про те, як знайти об'єм циліндра. Але спочатку потрібно визначитися з деякими теоретичними даними.
Буква-позначення
математична величина
V
обсяг
S
площа підстави
h
висота
r
радіус окружності
l
довжина твірної
?
кут між твірною і підставою
У будь-якому разі потрібно формула, в якій висота тіла, множиться на площу основи. Вона виглядає так: V = Sh Якщо потрібно дізнатися, як знайти об'єм циліндра прямого, то тут висота по довжині повністю збігається з твірною. Підставою найчастіше є коло, тоді його площа буде злічено за формулою: S = ?r 2 . Коли в задачі йдеться про еліптичному циліндрі, то буде потрібно така формула площі підстави: S = ? ab тут літерами a і b позначені мала і велика піввісь овалу. При вирішенні задач про похилому циліндрі потрібно ввести деякі доповнення в формулу. Наприклад, якщо відома висота, але йде мова про утворює і куті між нею і підставою. Тоді літеру h потрібно замінити таким виразом:
h = l * sin ? .
 Найчастіше в побуті нас оточують прямі кругові циліндри. Виміряти їх висоту зазвичай не складає труднощів. Потрібно просто прикласти лінійку збоку і виміряти відстань від низу до верху тіла. Це буде висота — h. З радіусом окружності все не так легко. Потрібно трохи згадати геометрію. Тут знадобиться аркуш паперу з прямим кутом і олівець. Що дає теорія з геометрії? Навколо прямокутного трикутника можна описати коло. Причому його прямий кут виявиться на ній, а гіпотенуза співпаде з діаметром. Потрібно взяти аркуш паперу і покласти його так, щоб прямий кут торкався краю підстави. Тоді дві його сторони, які утворюють цей кут, в деяких точках перетнуться з окружністю. У цих місцях потрібно зробити мітки. За ним провести відрізок. Він виявиться гіпотенузою і шуканим діаметром основи циліндра. Як знайти об'єм циліндра, в нашому випадку? У формулі фігурує радіус. Він дорівнює половині діаметра. Тобто довжину отриманого відрізка потрібно розділити на два. Залишилося тільки підставити результати вимірювань у формулу обсягу і порахувати. Причому врахувати, що відповідь вийде в см 3 . Якщо обсяг потрібно дізнатися в кубічних метрах, то число потрібно буде розділити на мільйон. Щоб отримати обсяг у літрах, дільником виявиться тисяча.
Найчастіше в побуті нас оточують прямі кругові циліндри. Виміряти їх висоту зазвичай не складає труднощів. Потрібно просто прикласти лінійку збоку і виміряти відстань від низу до верху тіла. Це буде висота — h. З радіусом окружності все не так легко. Потрібно трохи згадати геометрію. Тут знадобиться аркуш паперу з прямим кутом і олівець. Що дає теорія з геометрії? Навколо прямокутного трикутника можна описати коло. Причому його прямий кут виявиться на ній, а гіпотенуза співпаде з діаметром. Потрібно взяти аркуш паперу і покласти його так, щоб прямий кут торкався краю підстави. Тоді дві його сторони, які утворюють цей кут, в деяких точках перетнуться з окружністю. У цих місцях потрібно зробити мітки. За ним провести відрізок. Він виявиться гіпотенузою і шуканим діаметром основи циліндра. Як знайти об'єм циліндра, в нашому випадку? У формулі фігурує радіус. Він дорівнює половині діаметра. Тобто довжину отриманого відрізка потрібно розділити на два. Залишилося тільки підставити результати вимірювань у формулу обсягу і порахувати. Причому врахувати, що відповідь вийде в см 3 . Якщо обсяг потрібно дізнатися в кубічних метрах, то число потрібно буде розділити на мільйон. Щоб отримати обсяг у літрах, дільником виявиться тисяча. 
Що потрібно знати про циліндрі?
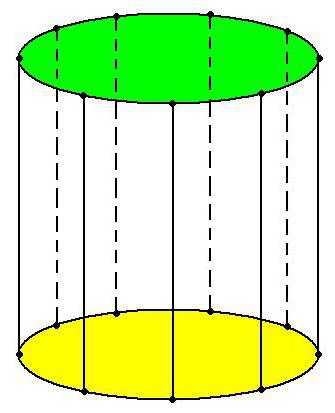
Геометричне тіло, про який ми говоримо, що утворюється в результаті обертання прямокутника навколо однієї з його сторін, і завжди буде прямим. Тобто кут між твірною циліндра і його підставою в даному випадку дорівнює 90 градусам. Якщо виконати це просте рух не вдається, і кут вже не 90 градусів, то йдеться про похилому циліндрі.
Як називаються окремі елементи циліндра і що про них відомо?
Відрізки, які з'єднують попарно відповідні точки на двох підставах, називаються утворюють. У будь-якого циліндра вони рівні і паралельні один одному. Якщо він прямий, довжина твірної збігається з висотою тіла. В основі може лежати коло або еліпс, тоді циліндр буде круговим або еліптичним відповідно. У формулах цей факт потрібно врахувати. Тому що найчастіше вони даються для кругового циліндра. В еліптичному, до того як обчислити об'єм циліндра, потрібно буде дізнатися, за якою формулою визначити площу овалу.Формули об'єму для прямого і похилого циліндрів
Тут і далі прийняті такі позначення.Буква-позначення
математична величина
V
обсяг
S
площа підстави
h
висота
r
радіус окружності
l
довжина твірної
?
кут між твірною і підставою
У будь-якому разі потрібно формула, в якій висота тіла, множиться на площу основи. Вона виглядає так: V = Sh Якщо потрібно дізнатися, як знайти об'єм циліндра прямого, то тут висота по довжині повністю збігається з твірною. Підставою найчастіше є коло, тоді його площа буде злічено за формулою: S = ?r 2 . Коли в задачі йдеться про еліптичному циліндрі, то буде потрібно така формула площі підстави: S = ? ab тут літерами a і b позначені мала і велика піввісь овалу. При вирішенні задач про похилому циліндрі потрібно ввести деякі доповнення в формулу. Наприклад, якщо відома висота, але йде мова про утворює і куті між нею і підставою. Тоді літеру h потрібно замінити таким виразом:
h = l * sin ? .

Як бути, якщо потрібно визначити обсяг на практиці?
У завданнях звичайно вже відомі значення кута або висоти з твірною. А можливо, якісь інші елементи, через які їх можна знайти. У житті доводиться робити вимірювання самостійно. Тоді питання про те, як визначити обсяг циліндра, зводиться до того, щоб правильно зробити його вимірювання висоти і радіусу. Для цього будуть потрібні: лінійка, олівець і прямокутний аркуш паперу.

Завдання
Умова. Дано два циліндра. Висота першого в два рази більше другого. Радіус другого вдвічі більше, ніж у першого. Необхідно дізнатися, у скільки разів обсяг першого циліндра більше або мегьше обсягу другого. Рішення. Спочатку потрібно ввести позначення. Нехай висота і радіус першого тіла будуть мати індекс 1 а другого — 2. Тепер можна записати дані в умові значення у вигляді виразів: h 1 = 2h 2 і r 2 = 2r 1 . Формули об'ємів обох циліндрів приймуть такий вигляд: v 1 = ? r 1 2 h 1 і v 2 = ? r 2 2 h 2 . В задачі потрібно знайти: v 1 : v 2 = (? r 1 2 h 1 ) : (? r 2 2 h 2 ). Після скорочення пі заміни h 1 і r 2 введеними виразами, виходить: v 1 : v 2 = (r 1 2 2h 2 ) : (4r 1 2 h 2 ). Тобто v 1 : v 2 = 1 : 2. Це означає, що обсяг першого циліндра в два рази менше. Відповідь. v 1 = v 2 : 2.Читайте також
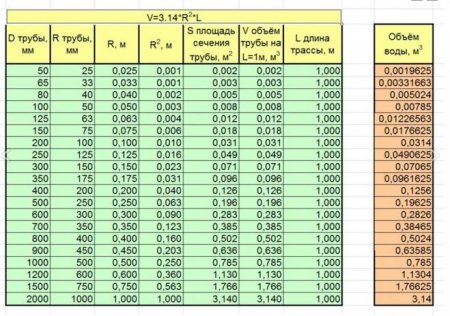
Дім
Обсяг труби в літрах: як обчислити і які формули краще підібрати
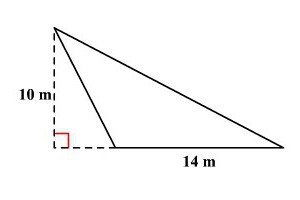
НАУКА
Як обчислити площу трикутника
НАУКА
Проста задача: як знайти периметр?
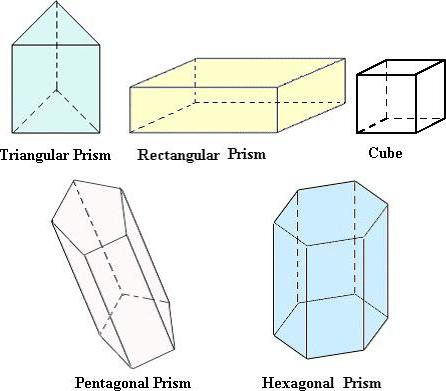
НАУКА
Як розрахувати обсяг різних геометричних тіл?
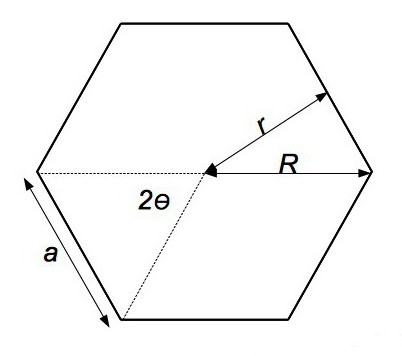
НАУКА
Як дізнатися площу багатокутника?
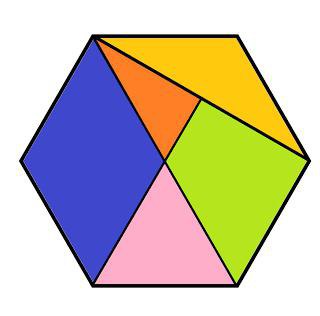
НАУКА
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
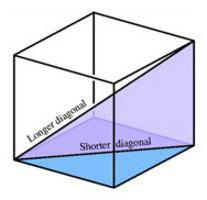
НАУКА
Діагональ куба: що це таке і як її знайти?
НАУКА
Циліндр. Види, обсяг циліндра, площа поверхні
