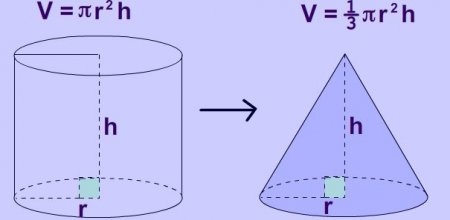
Як розрахувати обсяг різних геометричних тіл?
У курсі стереометрії одне з головних питань - як розрахувати обсяг того чи іншого геометричного тіла. Все починається з простого паралелепіпеда і закінчується кулею. В житті теж часто доводиться стикатися з подібними завданнями. Наприклад, щоб розрахувати об'єм води, яка міститься у відро чи бочку. Це значення - завжди додатне число. Якщо тіло вдається розділити на частини так, щоб не було перетинів, то загальний обсяг виявляється рівним сумі об'ємів частин. У рівних тіл однакові обсяги. Якщо менше тіло повністю поміщається в більшому, то обсяг першого менше, ніж другого.
Позначення
Пояснення
а
ребро тіла, у якого вони всі рівні
V
обсяг
S 0
площа підстави
h
висота
r
радіус
В деяких формулах є інші величини. Про їх позначенні буде сказано при появі такої необхідності.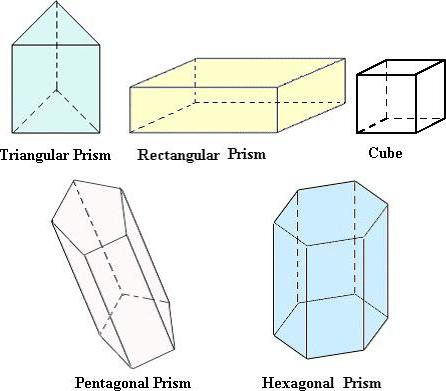 Відрізнятися буде тільки S 0 . У випадку з параллелепипедом вона розраховується, як для прямокутника або квадрата. У призмі підставою може виявитися трикутник, паралелограм, довільний чотирикутник або інший багатокутник. Для куба формула істотно спрощується, тому що всі його виміри дорівнюють: V = а 3 .
Відрізнятися буде тільки S 0 . У випадку з параллелепипедом вона розраховується, як для прямокутника або квадрата. У призмі підставою може виявитися трикутник, паралелограм, довільний чотирикутник або інший багатокутник. Для куба формула істотно спрощується, тому що всі його виміри дорівнюють: V = а 3 . 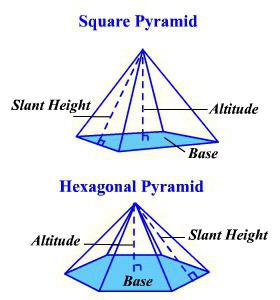 Тетраедр є приватним випадком трикутної піраміди. У нього всі ребра рівні. Тому знову виходить спрощена формула: V = (а 3 * ?2) /12 або V = 1/ 3 S 0 h Усіченої піраміда стає тоді, коли у неї зрізана верхня частина. Тому її об'єм дорівнює різниці двох пірамід: тієї, яка була б цілою, і віддаленої верхівки. Якщо є можливість дізнатися обидва підстави такої піраміди (S 1 — більшу і S 2 — менше), то зручно користуватися такою формулою для розрахунку обсягу:
Тетраедр є приватним випадком трикутної піраміди. У нього всі ребра рівні. Тому знову виходить спрощена формула: V = (а 3 * ?2) /12 або V = 1/ 3 S 0 h Усіченої піраміда стає тоді, коли у неї зрізана верхня частина. Тому її об'єм дорівнює різниці двох пірамід: тієї, яка була б цілою, і віддаленої верхівки. Якщо є можливість дізнатися обидва підстави такої піраміди (S 1 — більшу і S 2 — менше), то зручно користуватися такою формулою для розрахунку обсягу:
V = 1/3 * h * (S 1 + ?(S 1 S 2 ) + S 2 ).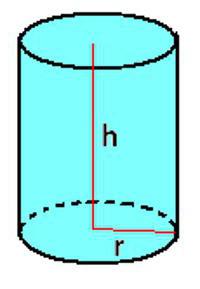 Дещо складніше йде справа з конусом. Для нього існує формула: V = 1/3 ? * r 2 * h. Вона дуже схожа на ту, що вказана для циліндра, тільки значення зменшено в три рази. Так само, як з усіченою пірамідою, справа йде непросто з конусом, який має дві підстави. Формула для обчислення об'єму конуса виглядає так: V = 1/3 ? * h * (r 1 2 + r 1 r 2 + r 2 2 ). Тут r 1 — радіус нижньої основи, r 2 — верхнього (меншого).
Дещо складніше йде справа з конусом. Для нього існує формула: V = 1/3 ? * r 2 * h. Вона дуже схожа на ту, що вказана для циліндра, тільки значення зменшено в три рази. Так само, як з усіченою пірамідою, справа йде непросто з конусом, який має дві підстави. Формула для обчислення об'єму конуса виглядає так: V = 1/3 ? * h * (r 1 2 + r 1 r 2 + r 2 2 ). Тут r 1 — радіус нижньої основи, r 2 — верхнього (меншого). 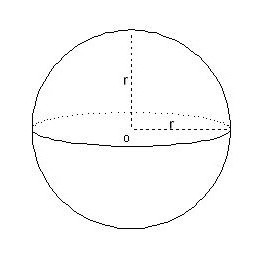 В задачах часто є питання про те, як розрахувати об'єм кульового сегмента — частини сфери, яка як би зрізана паралельно діаметру. У цьому випадку на виручку прийде така формула: V = ? h 2 * (r - h/3). У ній за h взята висота сегмента, тобто та частина, яка йде по радіусу кулі. Сектор ділиться на дві частини: конус і кульовий сегмент. Тому його обсяг визначається як сума цих тел. після перетворень Формула виглядає так: V = 2/3 ?r 2 * h. Тут h також висота сегмента.
В задачах часто є питання про те, як розрахувати об'єм кульового сегмента — частини сфери, яка як би зрізана паралельно діаметру. У цьому випадку на виручку прийде така формула: V = ? h 2 * (r - h/3). У ній за h взята висота сегмента, тобто та частина, яка йде по радіусу кулі. Сектор ділиться на дві частини: конус і кульовий сегмент. Тому його обсяг визначається як сума цих тел. після перетворень Формула виглядає так: V = 2/3 ?r 2 * h. Тут h також висота сегмента.
V 1 = 2 ? r 3 ; V 3 = 2/3 ? r 3 . Формула для об'єму кулі не змінюється, тому що в ній не фігурує висота. Тепер залишилося записати відношення обсягів і провести скорочення 2? і r 3 . Виходить, що V 1 : V 2 : V 3 = 1 : 2/3 : 1/3. Ці числа легко призвести до запису 3 : 2 : 1. Відповідь. V 1 : V 2 : V 3 = 3 : 2 : 1. Про об'єм кулі Умова: є два кавуна радіусами 15 і 20 см; як їх вигідніше з'їсти: перший вчотирьох або другий увісьмох? Рішення. Щоб відповісти на це питання, потрібно знайти відношення об'ємів частин, які дістануться від кожного кавуна. Беручи до уваги, що вони — кулі, потрібно записати дві формули для обсягів. Потім врахувати, що від першого кожному дістанеться тільки четверта частина, а від другого - восьма. Залишилося записати відношення обсягів частин. Воно буде виглядати так: (V 1 : 4) /(V 2 : 8) = (1/3 ? r 1 3 ) /(1/6 ? r 2 3 ). Після перетворення залишається тільки дріб: (2 r 1 3 ) /r 2 3 . Після підстановки значень і обчислення виходить дріб 6750/8000. З неї зрозуміло, що частина від першого кавуна буде менше, ніж від другої. Відповідь. Вигідніше з'їсти восьму частину від кавуна з радіусом 20 див. Про обсяги піраміди і куба Умова: є піраміда з глини з прямокутним підставою 8Х9 см і висотою 9 см; з цього ж шматка глини зробили куб; чому одно його ребро? Рішення. Якщо позначити сторони прямокутника літерами в і с, то площа основи піраміди обчислюється, як їх добуток. Тоді формула для її обсягу: V 1 = 1/3 * вс * h. Формула для об'єму куба написана в статті вище. Ці два значення дорівнюють: V 1 = V 2 . Залишилося прирівняти праві частини формул і зробити необхідні обчислення. Виходить, що ребро куба дорівнює 6 див. Відповідь. а = 6 див. Про об'єм паралелепіпеда Умова: потрібно зробити ящик місткістю 096 м 3 відомі його ширина і довжина - 12 і 08 метра; якою має бути його висота? Рішення. Оскільки підстава паралелепіпеда - прямокутники, його площа визначається як добуток довжини (а) на ширину (в). Тому формула для обсягу виглядає так: V = а * в * н З неї легко визначити висоту, розділивши обсяг на площу. Вийде, що висота повинна бути дорівнює 1 м. Відповідь. Висота ящика дорівнює одному метру.
Властивості, справедливі для обсягу кожного тіла
Загальні позначення для всіх тіл
У кожному з них є ребра і підстави, в них будуються висоти. Тому такі елементи для них однаково позначені. Саме так вони записані у формулах. Як розрахувати обсяг кожного з тіл - дізнаємося далі застосуємо на практиці нові вміння.Позначення
Пояснення
а
ребро тіла, у якого вони всі рівні
V
обсяг
S 0
площа підстави
h
висота
r
радіус
В деяких формулах є інші величини. Про їх позначенні буде сказано при появі такої необхідності.
Призма, паралелепіпед (прямий і похилий) і куб
Ці тіла об'єднані, тому що зовні дуже схожі, і формули того, як розрахувати обсяг, ідентичні: V = S 0 * h.
Піраміда, тетраедр, усічена піраміда
Для першого з зазначених тел існує така формула, щоб обчислити об'єм: V = 1/3 * S 0 * н.
V = 1/3 * h * (S 1 + ?(S 1 S 2 ) + S 2 ).
Циліндр, конус і усічений конус
Якщо потрібно розрахувати об'єм циліндра, можна скористатися формулою, яка вказана для призми. Іноді зручно записати її в такому вигляді: V =? * r 2 * h.
Куля, кульові сегменти і сектор
Це найбільш складні для запам'ятовування формул. Для об'єму кулі вона виглядає так: V = 4/3 ? *r 3 .
Приклади завдань
Про об'єми циліндра, кулі і конуса Умова: діаметр циліндра (1 тіло) дорівнює його висоті, діаметру кулі (2 тіло) і висоті конуса (3 тіло); перевірити пропорційність обсягів V 1 : V 2 : V 3 = 3:2:1 Рішення. Спочатку потрібно записати три формули для обсягів. Потім врахувати, що радіус — це половина діаметра. Тобто висота дорівнює двом радіусам: h = 2r. Зробивши просту заміну виходить, що формули для обсягів будуть мати такий вигляд:V 1 = 2 ? r 3 ; V 3 = 2/3 ? r 3 . Формула для об'єму кулі не змінюється, тому що в ній не фігурує висота. Тепер залишилося записати відношення обсягів і провести скорочення 2? і r 3 . Виходить, що V 1 : V 2 : V 3 = 1 : 2/3 : 1/3. Ці числа легко призвести до запису 3 : 2 : 1. Відповідь. V 1 : V 2 : V 3 = 3 : 2 : 1. Про об'єм кулі Умова: є два кавуна радіусами 15 і 20 см; як їх вигідніше з'їсти: перший вчотирьох або другий увісьмох? Рішення. Щоб відповісти на це питання, потрібно знайти відношення об'ємів частин, які дістануться від кожного кавуна. Беручи до уваги, що вони — кулі, потрібно записати дві формули для обсягів. Потім врахувати, що від першого кожному дістанеться тільки четверта частина, а від другого - восьма. Залишилося записати відношення обсягів частин. Воно буде виглядати так: (V 1 : 4) /(V 2 : 8) = (1/3 ? r 1 3 ) /(1/6 ? r 2 3 ). Після перетворення залишається тільки дріб: (2 r 1 3 ) /r 2 3 . Після підстановки значень і обчислення виходить дріб 6750/8000. З неї зрозуміло, що частина від першого кавуна буде менше, ніж від другої. Відповідь. Вигідніше з'їсти восьму частину від кавуна з радіусом 20 див. Про обсяги піраміди і куба Умова: є піраміда з глини з прямокутним підставою 8Х9 см і висотою 9 см; з цього ж шматка глини зробили куб; чому одно його ребро? Рішення. Якщо позначити сторони прямокутника літерами в і с, то площа основи піраміди обчислюється, як їх добуток. Тоді формула для її обсягу: V 1 = 1/3 * вс * h. Формула для об'єму куба написана в статті вище. Ці два значення дорівнюють: V 1 = V 2 . Залишилося прирівняти праві частини формул і зробити необхідні обчислення. Виходить, що ребро куба дорівнює 6 див. Відповідь. а = 6 див. Про об'єм паралелепіпеда Умова: потрібно зробити ящик місткістю 096 м 3 відомі його ширина і довжина - 12 і 08 метра; якою має бути його висота? Рішення. Оскільки підстава паралелепіпеда - прямокутники, його площа визначається як добуток довжини (а) на ширину (в). Тому формула для обсягу виглядає так: V = а * в * н З неї легко визначити висоту, розділивши обсяг на площу. Вийде, що висота повинна бути дорівнює 1 м. Відповідь. Висота ящика дорівнює одному метру.
Читайте також
Дім
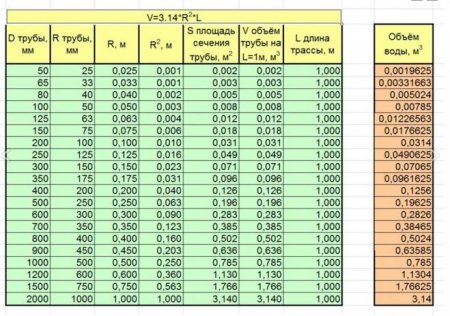
Обсяг труби в літрах: як обчислити і які формули краще підібрати

НАУКА
Робота електричного струму: формули та завдання по темі
НАУКА
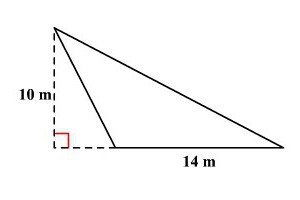
Як обчислити площу трикутника
НАУКА
Проста задача: як знайти периметр?
НАУКА
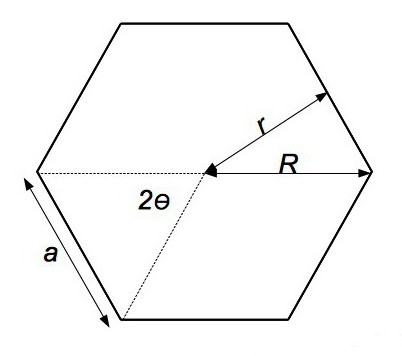
Як дізнатися площу багатокутника?
НАУКА
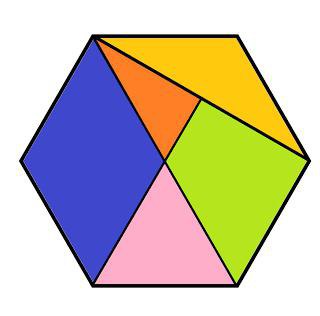
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
НАУКА
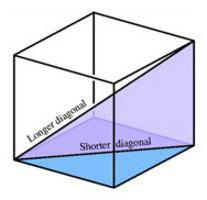
Діагональ куба: що це таке і як її знайти?
НАУКА
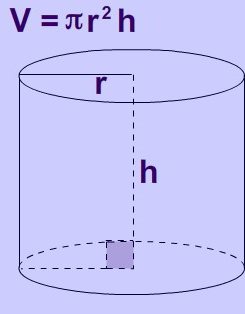
Як знайти об'єм циліндра: формули і завдання