Як дізнатися площу багатокутника?
В задачах геометрії часто потрібно обчислити площу багатокутника. Причому він може мати досить різноманітну форму – від всім знайомого трикутника до деякого n-кутника з якимось неймовірним числом вершин. До того ж ці багатокутники бувають опуклими або увігнутими. У кожній конкретній ситуації покладається відштовхуватися від зовнішнього вигляду фігури. Так вийде вибрати оптимальний шлях вирішення завдання. Фігура може виявитися правильною, що істотно спростить розв'язування задачі.
трикутник; чотирикутник; п'яти - або шестикутник і так далі. Така фігура неодмінно буде характеризуватися двома положеннями: Суміжні сторони не належать одній прямій. У несуміжних відсутні спільні точки, тобто вони не перетинаються. Щоб зрозуміти, які вершини є сусідніми, потрібно подивитися, чи належать вони одній стороні. Якщо так, то сусідні. В інакше їх можна буде з'єднати відрізком, який необхідно назвати діагоналлю. Їх можна провести тільки в багатокутниках, у яких більше трьох вершин.
S = 1/2 * а * н, де а — сторона, н — висота до неї; S = 1/2 * а * в * sin (А), де а, в — сторінs трикутника, А — кут між відомими сторонами; S = ?(p * (p - a) * (p -) * (p - c)), де з — сторона трикутника, до вже позначених двом, р — півпериметр, тобто сума всіх трьох сторін, поділена на два. 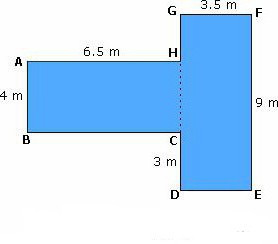 Фігура з чотирма вершинами може виявитися паралелограмом:
Фігура з чотирма вершинами може виявитися паралелограмом: S = а * н; S = 1/2 * d 1 * d 2 * sin(?), де d 1 і d 2 — діагоналі, ? — кут між ними; S = a * в * sin(?). Формула для площі трапеції: S = п * (a + в) /2 де а і в — довжини підстав. 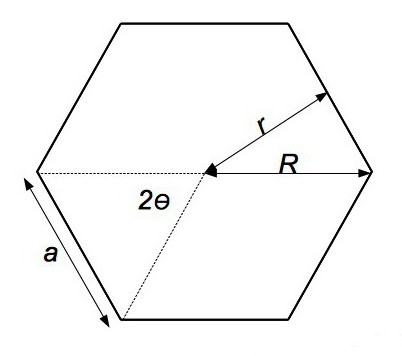 З неї легко отримати таку, яка стане в нагоді для приватних випадків:
З неї легко отримати таку, яка стане в нагоді для приватних випадків: трикутника: S = (3?3)/4 * R 2 ; квадрата: S = 2 * R 2 ; шестикутника: S = (3?3)/2 * R 2 . розбити його на прості фігури, наприклад, трикутники, щоб вони не перетиналися; обчислити їх площі за будь-якою формулою; скласти всі результати. 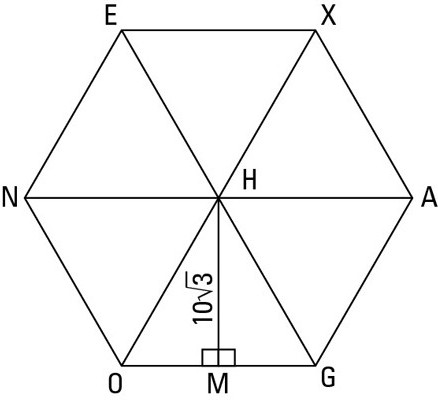
Трохи теорії про багатокутниках
Якщо провести три або більше пересічних прямих, то вони утворюють деяку фігуру. Саме вона є гратки. За кількістю точок перетину стає ясно, скільки вершин у нього буде. Вони дають назву вийшла фігури. Це може бути:Які їх види існують?
Багатокутник, у якого більше чотирьох кутів, може бути опуклим або увігнутим. Відмінність останнього в тому, що деякі його вершини можуть лежати по різні сторони від прямої, проведеної через довільну сторону багатокутника. В опуклому завжди всі вершини лежать з одного боку від такої прямої. У шкільному курсі геометрії велика частина часу приділяється саме помітних фігур. Тому в задачах потрібно дізнатися площа опуклого многокутника. Тоді існує формула через радіус описаної окружності, яка дозволяє знайти шукану величину для будь-якої фігури. В інших випадках однозначного вирішення не існує. Для трикутника формула одна, а для квадрата або трапеції зовсім інші. У ситуаціях, коли фігура неправильна або вершин дуже багато, прийнято розділяти їх на прості та знайомі.Як вчинити, якщо фігура має три або чотири вершини?
У першому випадку він виявиться трикутником, можна скористатися однією з формул:
Як вчинити з правильним гратки, у якого більше чотирьох вершин?
Для початку така фігура характеризується тим, що в ній всі сторони рівні. Плюс до цього, у багатокутника однакові кути. Якщо навколо такої фігури описати окружність, то її радіус співпаде з відрізком від центру багатокутника до однієї з вершин. Тому для того щоб обчислити площу правильного багатокутника з довільним числом вершин, буде потрібно така формула: S n = 1/2 * n * R n 2 * sin (360?/n), де n — кількість вершин багатокутника.
Ситуація з неправильною фігурою
Виходом для того, як дізнатися площа многокутника, якщо він не є правильним і його не можна віднести ні до одного з відомих раніше фігур, є алгоритм:Що робити, якщо в задачі дано координати вершин многокутника?
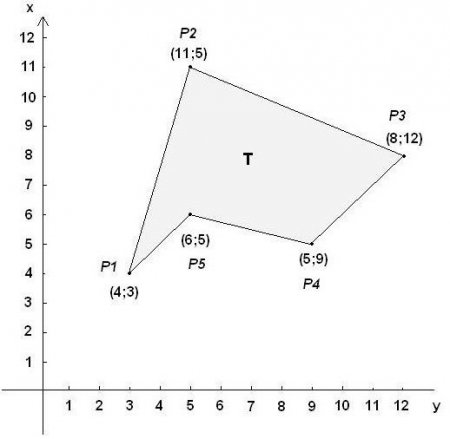
Тобто відомий набір пар чисел для кожної точки, які обмежують сторони фігури. Зазвичай вони записуються як (x 1 ; y 1 ) для першої, (x 2 ; y 2 ) — для другої, а n-а вершина має такі значення (x n ; y n ). Тоді площа багатокутника визначається, як сума n доданків. Кожне з них виглядає так: ((y i+1 +y i )/2) * (x i+1 - x i ). У цьому виразі i змінюється від одиниці до n. Варто зазначити, що знак результату буде залежати від обходу фігури. При використанні зазначеної формули і рух за годинниковою стрілкою відповідь буде виходити негативним.Приклад завдання
Умова. Координати вершин задані такими значеннями (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Потрібно обчислити площу багатокутника. Рішення. За формулою, зазначеною вище, перший доданок буде дорівнює (1.8 + 0.6)/2 * (3.6 - 2.1). Тут потрібно просто взяти значення для игрека і ікса від другої і першої точок. Нескладний розрахунок призведе до результату 1.8. Другий доданок аналогічно виходить: (2.2 + 1.8)/2 * (2.3 - 3.6) = -2.6. При вирішенні подібних завдань не варто лякатися негативних величин. Все йде так, як треба. Це планомірно. Подібним чином виходять значення для третього (029), четвертого (-6365) і п'ятого доданків (296). Тоді підсумкова площа дорівнює: 1.8 + (-2.6) + 029 + (-6365) + 296 = - 3915.
Рада з рішенням задачі, для якої багатокутник зображений на папері в клітку
Найчастіше спантеличує те, що в даних є тільки розмір клітинки. Але виявляється, що більше відомостей не потрібно. Рекомендацією до вирішення такої задачі є розбивання фігури на безліч трикутників, прямокутників. Їх площі досить просто порахувати по довжинам сторін, які потім легко скласти. Але часто є більш простий підхід. Він полягає в тому, щоб домалювати фігуру до прямокутника і обчислити значення його площі. Потім порахувати площі тих елементів, які виявилися зайвими. Відняти їх з загального значення. Цей варіант деколи передбачає декілька меншу кількість дій.Читайте також
НАУКА
Плоскі та об'ємні геометричні фігури
НАУКА
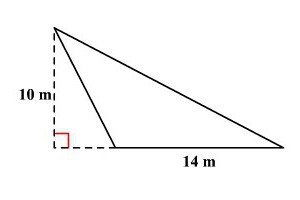
Як обчислити площу трикутника
НАУКА
Проста задача: як знайти периметр?
НАУКА
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
НАУКА
Діагональ куба: що це таке і як її знайти?
НАУКА
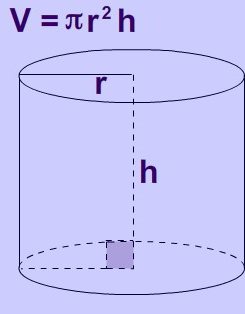
Як знайти об'єм циліндра: формули і завдання
НАУКА
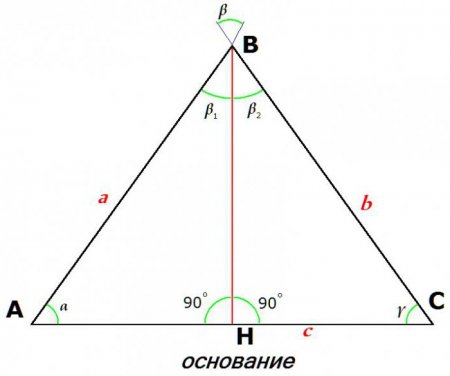
Ознаки, складові елементи та властивості рівнобедреного трикутника

НАУКА
Про те, як порахувати квадратні метри, і що таке площа приміщення