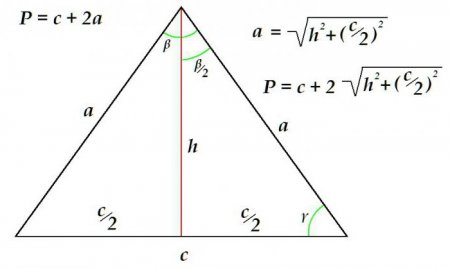
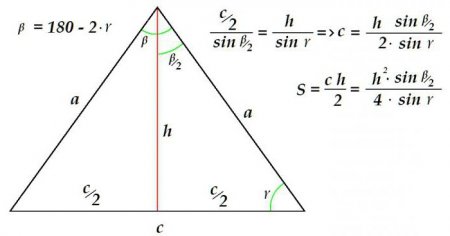
Ознаки, складові елементи та властивості рівнобедреного трикутника
Перші історики нашої цивілізації – стародавні греки - згадують Єгипет як місце зародження геометрії. Важко з ними не погодитися, знаючи, з якою приголомшливою точністю зведені гігантські усипальниці фараонів. Взаємне розташування площин пірамід, їх пропорції, орієнтація по сторонам світу – досягти такої досконалості було б немислимо, не знаючи основ геометрії.
Саме слово "геометрія" можна перекласти як «вимірювання землі». Причому слово «земля» виступає не як планета – частина Сонячної системи, а як площину. Розмітка площ під ведення сільського господарства, швидше за все, і є вихідною основою науки про геометричні фігури, їх види та властивості. Трикутник – найпростіша просторова фігура планіметрії, що містить всього три точки - вершини (менше не буває). Основа основ, може бути, тому і ввижається в ньому щось таємниче і давнє. Всевидюче око всередині трикутника – один із самих ранніх з відомих окультних знаків, причому географія його поширення і тимчасові рамки просто вражають уяву. Від стародавніх єгипетської, шумерської, ацтекської і інших цивілізацій до більш сучасних спільнот любителів окультизму, розкиданих по всій земній кулі.
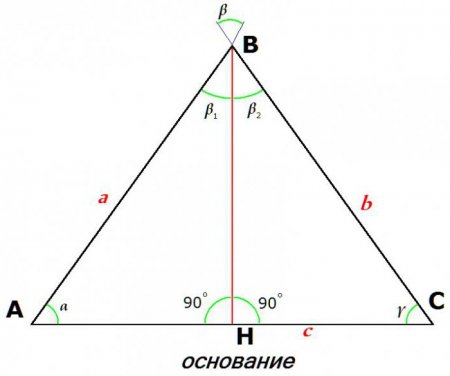
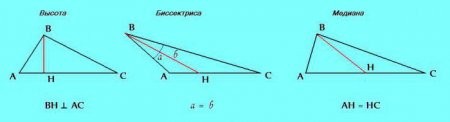
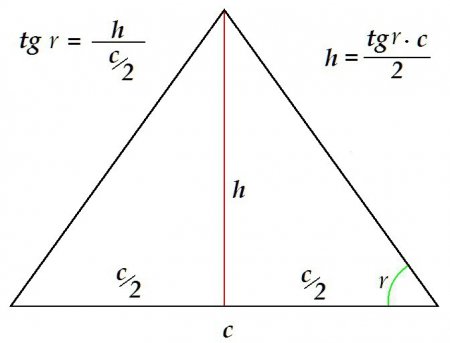
На даному малюнку a = b. Другий ознака рівнобедреного трикутника випливає з теореми синусів. Так як рівні сторони a і b, рівні і синуси їх протилежних кутів: a/sin ? = b/sin ?, звідки маємо: sin ? = sin ?. З рівності синусів слід рівність кутів: ? = ?. Отже, другою ознакою рівнобедреного трикутника є рівність двох кутів, прилеглих до основи. Третя ознака. У трикутнику розрізняють такі елементи, як висота, бісектриса і медіана. Якщо в процесі вирішення завдання з'ясовується, що в розглянутому трикутнику два будь-яких з цих елементів збігаються: висота з бісектрисою; бісектриса з медіаною; медіана з висотою - однозначно можна робити висновок, що трикутник рівнобедрений.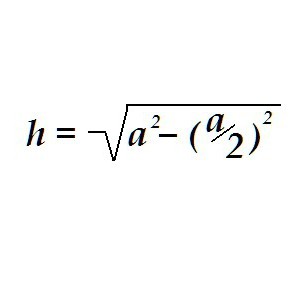 Можна визначити висоту й іншим шляхом, наприклад знаючи основу і прилеглий до нього кут.
Можна визначити висоту й іншим шляхом, наприклад знаючи основу і прилеглий до нього кут.
Саме слово "геометрія" можна перекласти як «вимірювання землі». Причому слово «земля» виступає не як планета – частина Сонячної системи, а як площину. Розмітка площ під ведення сільського господарства, швидше за все, і є вихідною основою науки про геометричні фігури, їх види та властивості. Трикутник – найпростіша просторова фігура планіметрії, що містить всього три точки - вершини (менше не буває). Основа основ, може бути, тому і ввижається в ньому щось таємниче і давнє. Всевидюче око всередині трикутника – один із самих ранніх з відомих окультних знаків, причому географія його поширення і тимчасові рамки просто вражають уяву. Від стародавніх єгипетської, шумерської, ацтекської і інших цивілізацій до більш сучасних спільнот любителів окультизму, розкиданих по всій земній кулі.
Якими бувають трикутники
Звичайний різносторонній трикутник – це замкнута геометрична фігура, що складається з трьох відрізків різної довжини і трьох кутів, жоден з яких не є прямим. Крім нього, розрізняють кілька особливих видів. Трикутник гострокутний має всі кути величиною менше 90 градусів. Іншими словами – всі кути такого трикутника гострі. Прямокутний трикутник, над яким у всі часи плакали школярі з-за великої кількості теорем, має один кут з величиною 90 градусів або, як його ще називають, прямий. Тупокутний трикутник відрізняється тим, що один з його кутів тупий, тобто величина його - більше 90 градусів. Рівносторонній трикутник має три сторони однакової довжини. У такої фігури рівні також всі кути. І нарешті, у рівнобедреного трикутника з трьох боків дві рівні між собою.Відмітні особливості
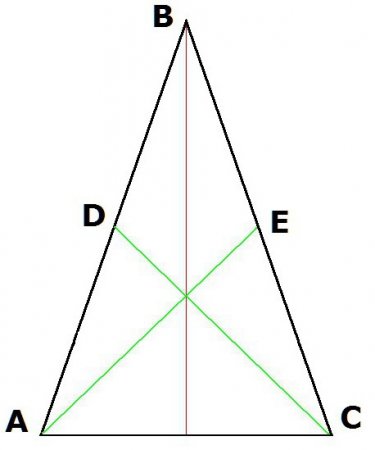
Властивості рівнобедреного трикутника визначають і його основне, головне, відмінність – рівність двох сторін. Ці рівні один одному боку прийнято називати стегнами (або, частіше, бічними сторонами), ну а третя сторона носить назву «основа».На даному малюнку a = b. Другий ознака рівнобедреного трикутника випливає з теореми синусів. Так як рівні сторони a і b, рівні і синуси їх протилежних кутів: a/sin ? = b/sin ?, звідки маємо: sin ? = sin ?. З рівності синусів слід рівність кутів: ? = ?. Отже, другою ознакою рівнобедреного трикутника є рівність двох кутів, прилеглих до основи. Третя ознака. У трикутнику розрізняють такі елементи, як висота, бісектриса і медіана. Якщо в процесі вирішення завдання з'ясовується, що в розглянутому трикутнику два будь-яких з цих елементів збігаються: висота з бісектрисою; бісектриса з медіаною; медіана з висотою - однозначно можна робити висновок, що трикутник рівнобедрений.
Геометричні властивості фігури
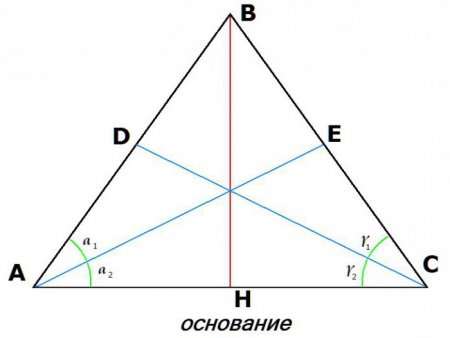
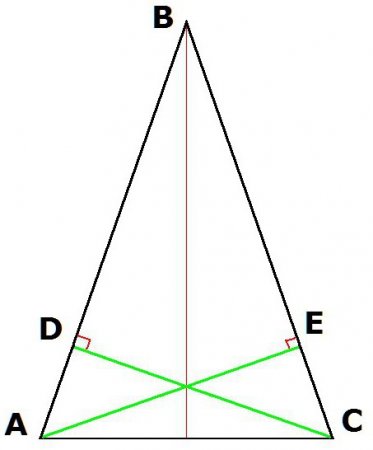
1. Властивості рівнобедреного трикутника. Одним з відмінних якостей фігури є рівність кутів, прилеглих до основи: ? = ?; <ВАС = <ВСА. 2. Ще одна властивість розглянуто вище: медіана, бісектриса і висота в равнобедренном трикутнику збігаються, якщо вони збудовані від його вершини до основи. 3. Рівність бісектрис, проведених з вершин при підставі: Якщо АЕ – бісектриса кута ВАС, а CD – бісектриса кута BCA, то: AE = DC. 4. Властивості рівнобедреного трикутника передбачають також рівність висот, які проведені з вершин при підставі. Якщо побудувати висоти трикутника АВС (де АВ = ВС) з вершин А і С, то отримані відрізки CD і АЕ будуть рівні. 5. Рівними також виявляться і медіани, проведені з кутів при підставі. Так, якщо АЕ і DC – медіани, тобто AD = DB, а BE = EC, то АЕ = DC.Висота рівнобедреного трикутника
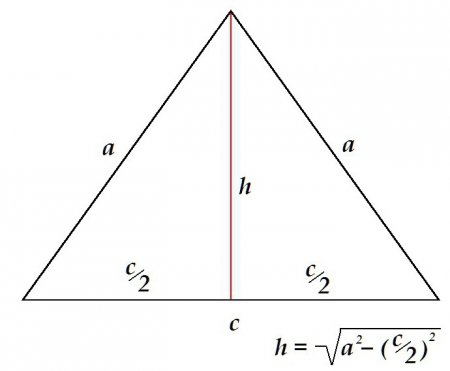
Рівність бокових сторін і кутів при них привносить деякі особливості обчислення довжин елементів розглянутої фігури. Висота в равнобедренном трикутнику ділить фігуру на 2 симетричних прямокутних трикутника, гипотенузами у яких виступають бічні сторони. Висота в такому разі визначається згідно з теоремою Піфагора, як катет. У трикутника можуть бути рівними всі три сторони, тоді він буде називатися рівностороннім. Висота в рівносторонньому трикутнику визначається аналогічно, лише для розрахунків достатньо знати лише одне значення – довжину сторони цього трикутника.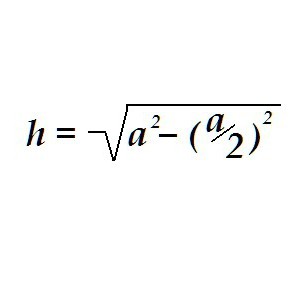
Медіана рівнобедреного трикутника
Розглянутий тип трикутника, завдяки геометричним особливостей, вирішується досить просто за мінімального набору вихідних даних. Так як медіана у равнобедренном трикутнику дорівнює його висоті, і його бісектрисі, то алгоритм її визначення нічим не відрізняється від порядку обчислення даних елементів. Наприклад, визначити довжину медіани можна по відомій бічній стороні і величиною кута при вершині.Як визначити периметр
Так як у розглянутій планиметрической фігури дві сторони завжди рівні, то для визначення периметра достатньо знати довжину підстави і довжину однієї зі сторін. Розглянемо приклад, коли потрібно визначити периметр трикутника за відомими основи і висоті. Периметр дорівнює сумі підстави та подвоєної довжини бічної сторони. Бічна сторона, у свою чергу, визначається за допомогою теореми Піфагора як гіпотенуза прямокутного трикутника. Довжина її дорівнює кореню квадратному із суми квадратів висоти і квадрата половини підстави.Площа рівнобедреного трикутника
Не викликає, як правило, труднощів і обчислення площі рівнобедреного трикутника. Універсальне правило визначення площі трикутника як половини твори підстави на його висоту стосується, звичайно ж, і в нашому випадку. Однак, властивості рівнобедреного трикутника знову полегшують завдання. Припустимо, що відомі висота і кут, прилеглий до основи. Необхідно визначити площу фігури. Зробити це можна таким способом. Так як сума кутів будь-якого трикутника дорівнює 180°, то визначити величину кута не складе праці. Далі, скориставшись пропорцією, складеної згідно з теоремою синусів, визначається довжина підстави трикутника. Все, основа і висота – достатні дані для визначення площі - є.Інші властивості рівнобедреного трикутника
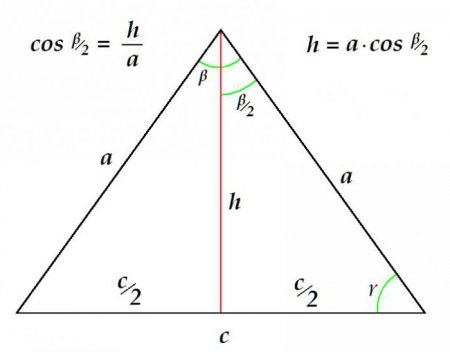
Положення центра кола, описаного навколо рівнобедреного трикутника, залежить від величини кута вершини. Так, якщо рівнобедрений трикутник гострокутний, центр кола розташовується всередині фігури. Центр кола, яка описана навколо тупоугольного рівнобедреного трикутника, лежить поза його. І, нарешті, якщо величина кута при вершині дорівнює 90°, центр лежить рівно на середині підстави, а через сама підстава проходить діаметр окружності. Для того щоб визначити радіус окружності, описаної близько рівнобедреного трикутника, досить розділити довжину бічної сторони на подвоєний косинус половини величини кута при вершині.Читайте також

Компютер і інтернет
Як зробити в CSS трикутник: найзручніші способи
НАУКА
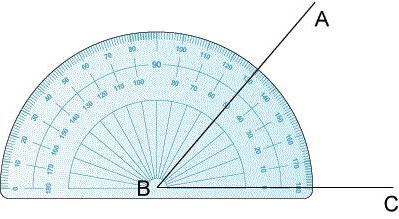
Розгорнутий кут в геометрії
НАУКА
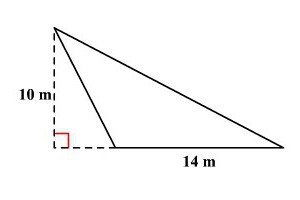
Як обчислити площу трикутника
НАУКА
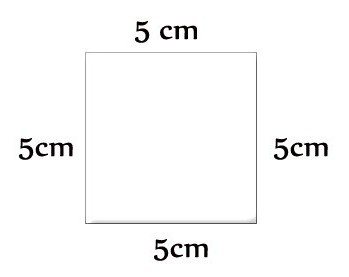
Проста задача: як знайти периметр?
НАУКА
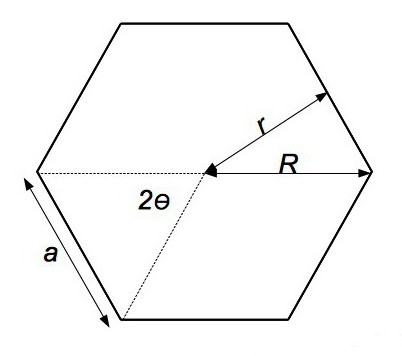
Як дізнатися площу багатокутника?
НАУКА
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
НАУКА
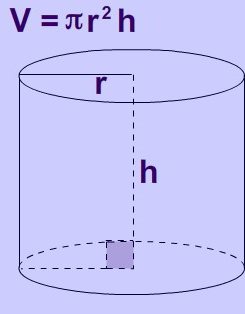
Як знайти об'єм циліндра: формули і завдання

НАУКА
Про те, як порахувати квадратні метри, і що таке площа приміщення