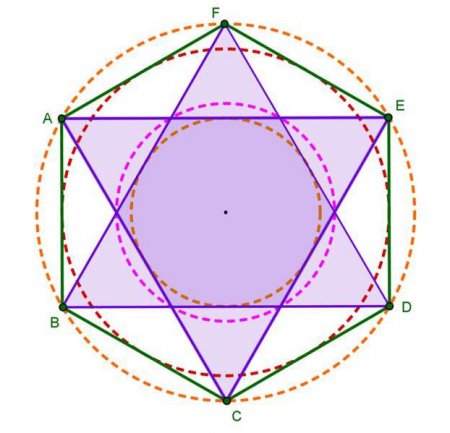
Що таке правильний шестикутник і які завдання з ним можуть бути пов'язані?
Найвідоміша фігура, у якої більше чотирьох кутів - це правильний шестикутник. В геометрії він часто використовується в задачах. А в житті саме такий вигляд мають стільники на зрізі.
По-третє, правильний шестикутник характеризується тим, що всі його сторони рівні. Причому кожен кут фігури теж має однакове значення. Щоб визначити суму всіх кутів, потрібно скористатися формулою: 180 * (n — 2). Тут n — число вершин фігури, тобто 6. Простий розрахунок дає значення в 720?. Тобто кожен кут дорівнює 120 градусам. У повсякденній діяльності правильний шестикутник зустрічається в сніжинці і гайці. Хіміки бачать її навіть в молекулі бензолу.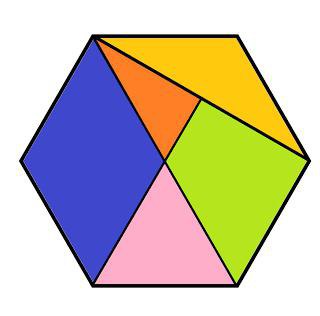
діагоналі фігури, проведені через центр, ділять її на шість трикутників, які є рівносторонніми; сторона правильного шестикутника має значення, яке співпадає з радіусом описаного біля нього кола; використовуючи таку фігуру, є можливість заповнити площину, причому між ними не вийде пропусків і не буде накладень.
В деяких формулах фігурують внутрішній кут, півпериметр і апофема (є перпендикуляром до середини будь-якої сторони з центру багатокутника). Для них використовуються букви: ?, р, m.
Для площі правильного шестикутника може знадобитися така: S = p * r = (a 2 * 3 ?3) /2.
Чим він відрізняється від неправильного?
По-перше, шестикутником є фігура з 6 вершинами. По-друге, він може бути опуклим або увігнутим. Перший відрізняється тим, що чотири вершини лежать по одну сторону від прямої, проведеної через дві інші.По-третє, правильний шестикутник характеризується тим, що всі його сторони рівні. Причому кожен кут фігури теж має однакове значення. Щоб визначити суму всіх кутів, потрібно скористатися формулою: 180 * (n — 2). Тут n — число вершин фігури, тобто 6. Простий розрахунок дає значення в 720?. Тобто кожен кут дорівнює 120 градусам. У повсякденній діяльності правильний шестикутник зустрічається в сніжинці і гайці. Хіміки бачать її навіть в молекулі бензолу.

Які властивості потрібно знати при вирішенні завдань?
До того, що зазначено вище, слід додати:Введені позначення
Традиційно сторона правильної геометричної фігури позначається латинською літерою «а». Для вирішення завдань потрібні ще площа і периметр, це S і P відповідно. У правильний шестикутник буває вписана окружність або описана близько нього. Тоді вводяться значення для їх радіусів. Позначаються вони відповідно літерами r та R.В деяких формулах фігурують внутрішній кут, півпериметр і апофема (є перпендикуляром до середини будь-якої сторони з центру багатокутника). Для них використовуються букви: ?, р, m.
Формули, які описують фігуру
Для розрахунку радіуса вписаного кола буде потрібно така: r = (a * ?3) /2 причому r = m. Тобто така ж формула буде і для апофеми. Оскільки периметр шестикутника — це сума всіх сторін, то він визначиться так: P = 6 * a. З урахуванням того, що сторона дорівнює радіусу описаного кола, для периметра існує така формула правильного шестикутника: P = 6 * R. З тієї, що наведена для радіуса вписаного кола, виводиться залежність між а і r. Тоді формула приймає такий вигляд: Р = 4 r * ?3.Для площі правильного шестикутника може знадобитися така: S = p * r = (a 2 * 3 ?3) /2.
Завдання
№ 1. Умова. Є правильна шестикутна призма, кожне ребро якої дорівнює 4 див. В неї вписано циліндр, обсяг якого необхідно дізнатися. Рішення. Об'єм циліндра визначається як добуток площі основи на висоту. Остання збігається з ребром призми. А вона дорівнює стороні правильного шестикутника. Тобто висота циліндра - теж 4 див. Щоб дізнатися площа його основи, потрібно обчислити радіус вписаного в шестикутник колу. Формула для цього зазначена вище. Отже, r = 2?3 (см). Тоді площа кола: S = ? * r 2 = 314 * (2?3 ) 2 = 3768 (см 2 ). Залишилося порахувати об'єм: V = 3768 * 4 = 15072 (см 3 ). Відповідь . V = 15072 см 3 . № 2. Умова. Обчислити радіус кола, яка вписана у правильний шестикутник. Відомо, що його сторона дорівнює ?3 см. Чому дорівнює його периметр? Рішення. Ця задача вимагає використання двох із зазначених формул. Причому їх необхідно застосовувати, навіть не видозмінюючи, просто підставити значення сторони і обчислити. Таким чином, радіус вписаного кола виходить рівним 15 см. Для периметра виявляється вірним таке значення: 6?3 див. Відповідь. r = 15 см, Р = 6?3 див. № 3. Умова. Радіус описаного кола дорівнює 6 див. Яке значення в цьому випадку буде у сторони правильного шестикутника? Рішення. З формули для радіусів вписаного в шестикутник колу легко виходить та, за якою потрібно обчислювати бік. Ясно, що радіус множиться на два і ділиться на корінь з трьох. Необхідно позбавитися від ірраціональності в знаменнику. Тому результат дій приймає такий вигляд: (12 ?3) /(?3 * ?3), тобто 4?3. Відповідь. а = 4?3 див.Читайте також
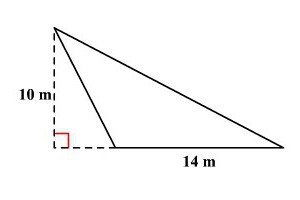
НАУКА
Як обчислити площу трикутника
НАУКА
Проста задача: як знайти периметр?
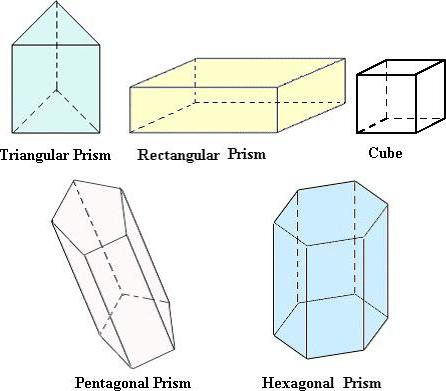
НАУКА
Як розрахувати обсяг різних геометричних тіл?
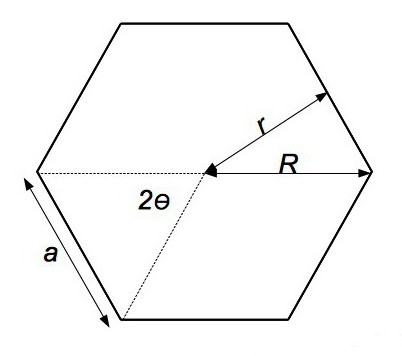
НАУКА
Як дізнатися площу багатокутника?
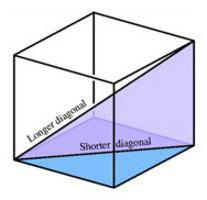
НАУКА
Діагональ куба: що це таке і як її знайти?
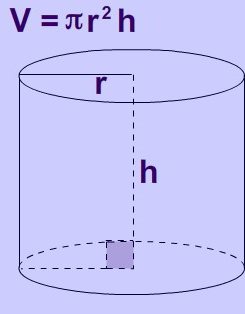
НАУКА
Як знайти об'єм циліндра: формули і завдання
НАУКА
Циліндр. Види, обсяг циліндра, площа поверхні
НАУКА
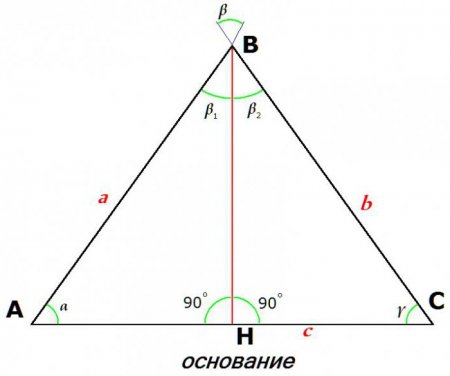
Ознаки, складові елементи та властивості рівнобедреного трикутника