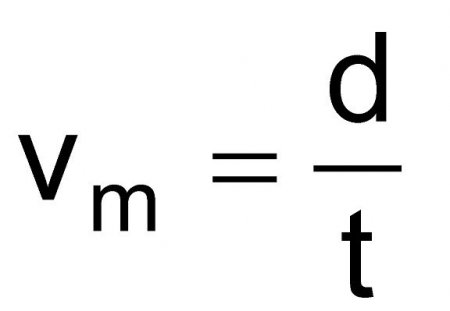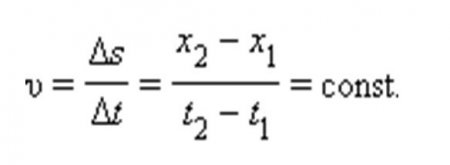Рівномірний рух. Формула рівномірного руху.
Знайомство з класичним курсом фізики починається з найпростіших законів, яким підкоряються тіла, переміщаються в просторі. Прямолінійний рівномірний рух – найпростіший вид зміни положення тіла в просторі. Такий рух вивчається в розділі кінематики.

При рівномірному переміщенні положення тіла в будь-який період часу визначається лише однією координатою x. Напрям руху тіла і вектор швидкості направлені уздовж осі х, при цьому початок руху можна відраховувати від нульової позначки. Тому аналіз переміщення тіла в просторі можна звести до проекції траєкторії руху на вісь ОХ і описувати процес алгебраїчними рівняннями.
 При чому ж тут рівномірний рух? Все дуже просто. На дуже малих проміжках шляху швидкість руху тіла цілком можна вважати рівномірним, з прямолінійною траєкторією. Таким чином, виникла блискуча можливість вивчити більш складні рухи, зводячи їх до простих. Так вивчалося рівномірний рух тіла по колу.
При чому ж тут рівномірний рух? Все дуже просто. На дуже малих проміжках шляху швидкість руху тіла цілком можна вважати рівномірним, з прямолінійною траєкторією. Таким чином, виникла блискуча можливість вивчити більш складні рухи, зводячи їх до простих. Так вивчалося рівномірний рух тіла по колу. 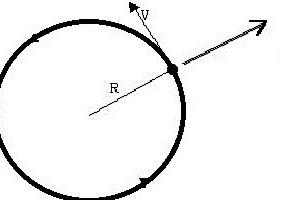 Як можна бачити, планета бере участь у двох різних рухах. Геометричне додавання швидкостей і дасть нам швидкість планети на даному відрізку шляху. Рівномірний рух – основа для подальшого вивчення кінематики і фізики в цілому. Це елементарний процес, до якого можна звести набагато більш складні переміщення. Але у фізиці, як і скрізь, велике починається з малого, і запускаючи в безповітряний простір космічні кораблі, керуючи підводними човнами, слід не забувати про тих простих дослідах, на яких Галілей колись перевіряв свої відкриття.
Як можна бачити, планета бере участь у двох різних рухах. Геометричне додавання швидкостей і дасть нам швидкість планети на даному відрізку шляху. Рівномірний рух – основа для подальшого вивчення кінематики і фізики в цілому. Це елементарний процес, до якого можна звести набагато більш складні переміщення. Але у фізиці, як і скрізь, велике починається з малого, і запускаючи в безповітряний простір космічні кораблі, керуючи підводними човнами, слід не забувати про тих простих дослідах, на яких Галілей колись перевіряв свої відкриття.
Противник Аристотеля
Галілео Галілей залишився в анналах історії як один з найвидатніших натуралістів часів пізнього Ренесансу. Він наважився перевіряти затвердження Аристотель – нечувана по тим часам єресь, бо вчення стародавнього мудреця всіляко підтримувалася церквою. Ідея рівномірного руху тоді не розглядалася – тіло або рухалося «взагалі», або знаходилась у стані спокою. Знадобилися численні експерименти для того, щоб пояснити природу руху.Досліди Галілея
Класичним прикладом вивчення руху став відомий експеримент Галілея, коли він кидав різні тяжкості зі знаменитої Пізанської вежі. В результаті цього експерименту з'ясувалося, що тіла, що мають різні маси, падають з однаковою швидкістю. Пізніше експеримент був продовжений в горизонтальній площині. Галілей запропонував, що будь-куля при відсутності тертя буде котитися з гори як завгодно довго, при цьому швидкість його так само буде постійною. Так, експериментальним шляхом, Галілео Галілей відкрив сутність першого закону Ньютона – при відсутності зовнішніх сил тіло рухається по прямій з постійною швидкістю. Прямолінійний рівномірний рух – це і є вираження першого закону Ньютона. В даний час різними видами руху займається особливий розділ фізики - кінематика. У перекладі з грецької дане найменування означає - вчення про рух.Нова система координат
Аналіз рівномірного руху був би неможливий без створення нового принципу визначення положення тіл у просторі. Зараз ми називаємо його прямолінійною системою координат. Автор її - відомий філософ і математик Рене Декарт, завдяки якому ми і називаємо систему координат декартовій. У такому вигляді дуже зручно представляти траєкторію руху тіла в тривимірному просторі і аналізувати таке переміщення, прив'язуючи положення тіла до координатним осям. Прямокутна система координат являє собою дві пересічні під прямим кутом прямі. Точка перетину зазвичай приймається за початок відліку вимірювань. Горизонтальна лінія називається абсцисою, вертикальна – ординатою. Оскільки ми живемо у тривимірному просторі, до площинний системі координат додають і третю вісь – її називають аплікат.
Визначення швидкості
Швидкість неможливо виміряти так, як ми вимірюємо відстань і час. Це завжди величина похідна, яка і записується у вигляді співвідношення. В самому загальному вигляді швидкість тіла дорівнює відношенню пройденої відстані до витраченому часу. Формула для швидкості має вигляд: Де d - пройдена відстань, t - витрачений час. Напрямок безпосередньо впливає на векторне позначення швидкості (величина, що визначає час – скаляр, тобто воно напряму не має).Уявлення про рівномірному русі
При рівномірному русі тіло рухається вздовж прямої з постійною швидкістю. Оскільки швидкість – це векторна величина, її властивості описуються не лише числом, але й напрямком. Тому краще уточнити визначення, і сказати, що швидкість рівномірного прямолінійного руху постійна по модулю і напрямом. Щоб описати прямолінійний рівномірний рух, достатньо використовувати декартову систему координат. В цьому випадку вісь ОХ буде зручно прокласти по напрямку руху.При рівномірному переміщенні положення тіла в будь-який період часу визначається лише однією координатою x. Напрям руху тіла і вектор швидкості направлені уздовж осі х, при цьому початок руху можна відраховувати від нульової позначки. Тому аналіз переміщення тіла в просторі можна звести до проекції траєкторії руху на вісь ОХ і описувати процес алгебраїчними рівняннями.
Рівномірний рух з точки зору алгебри
Припустимо, що в певний момент часу t 1 тіло знаходиться в точці на осі абсцис, координата якої дорівнює х 1 . Черга деякої проміжок часу тіло змінить своє місце розташування. Тепер координата його знаходження в просторі буде дорівнювати х 2 . Звівши розгляд руху тіла до його розташуванню на осі координат, можна визначити, що шлях, який пройшло тіло, дорівнює різниці початкової та кінцевої координати. Алгебраїчно це записується так: ?s = x 2 – x 1.Величина переміщення
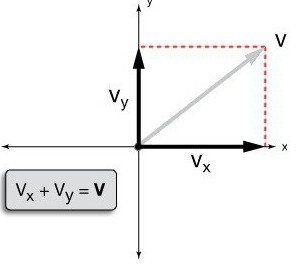
Величина, що визначає переміщення тіла, може бути і більше, і менше 0. Все залежить від того, в яку сторону щодо напрямку осі переміщалося тіло. У фізиці можна записувати і негативне, і позитивне переміщення – все залежить від обраної для відліку системи координат. Прямолінійний рівномірний рух відбувається зі швидкістю, яка описується формулою: При цьому швидкість буде більше нуля, якщо тіло рухається вздовж осі ОХ від нуля; менше нуля – якщо рух йде справа наліво по осі абсцис. Така коротка запис відображає суть рівномірного прямолінійного руху – якими б не були зміни координат, швидкість переміщення залишається незмінною. Галілею ми зобов'язані ще однією геніальною думкою. Аналізуючи рух тіла у світі, позбавленому тертя, вчений наполягав на тому, що сили і швидкості не залежать один від одного. Ця блискуча думка знайшла своє відображення у всіх існуючих законах руху. Так, сили, діючі на тіло, не залежать один від одного і діють так, ніби інших не існує. Застосовуючи це правило до аналізу руху тіла, Галілей зрозумів, що всю механіку процесу можна розкласти на сили, які складаються геометрично (векторно) або лінійно, якщо діють в одному напрямку. Приблизно це буде виглядати так:
Рівномірний рух по колу
Рівномірний і равноускоренное рух можна спостерігати в переміщенні планет по своїх орбітах. У цьому випадку планета бере участь у двох видах незалежних рухів: вона рівномірно переміщається по окружності і в теж час равноускоренно рухається до Сонця. Таке складне рух пояснюється силами, що діють на планети. Схема впливу планетарних сил представлена на малюнку:
Читайте також
НАУКА
Що таке напруженість електричного поля

НАУКА
Закон Архімеда: визначення і формула

НАУКА
Скільки годин у добі. Добу сонячні і зоряні

НАУКА
Досвід Штерна - експериментальне підтвердження теорії
НАУКА
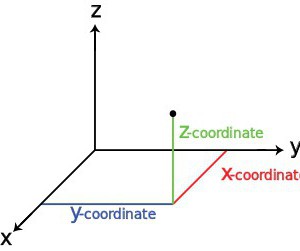
Тривимірний простір: вектори, координати

СПОРТ
Тренажер "Хаммер": призначення, особливості застосування, переваги та недоліки
НАУКА
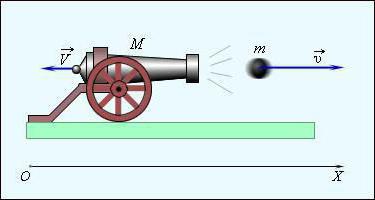
Імпульс тіла: означення і властивості

НАУКА
Кутова швидкість. Формула кутової швидкості